已知F1，F2分别为双曲线C：x2a2-y2b2=1（a>0，b>0）的左、右焦点，若点P是以F1F2为直径的圆与C右支的-个交点，F1P交C于另一点Q，且|PQ|=2|QF1|．则C的渐近线方程为（）A.y=±2xB.y=±12xC.y=

Question

已知F₁，F₂分别为双曲线C：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的左、右焦点，若点P是以F₁F₂为直径的圆与C右支的-个交点，F₁P交C于另一点Q，且|PQ|=2|QF₁|．则C的渐近线方程为（　　）

A. y=±2x

B. y=±

(1)/(2)x

C. y=±

√(2)x

D. y=±

(√(2))/(2)x

Answer 1

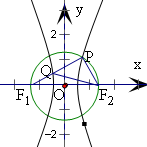由题意可得PF₁⊥PF₂，
可设|QF₁|=t，可得|PQ|=2t，
由双曲线的定义可得|PF₁|-|PF₂|=2a，
即有|PF₂|=3t-2a，
又连接QF₂，可得|QF₂|-|QF₁|=2a，
即有|QF₂|=t+2a，
在直角三角形PF₁F₂中，
|PF₁|²+|PF₂|²=|F₁F₂|²，
即为（3t）²+（3t-2a）²=4c²，①
又|PQ|²+|PF₂|²=|QF₂|²，
即有4t²+（3t-2a）²=（t+2a）²，②
由②可得，3t=4a，
代入①，可得16a²+4a²=4c²，
即有c=√(5)a，b=√(c2-a2)=2a，
即有渐近线方程为y=±2x．
故选：A．