早教吧作业答案频道 -->数学-->
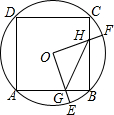
如图,边长为4的正方形ABCD内接于点O,点E是AB上的一动点(不与A、B重合),点F是BC上的一点,连接OE、OF,分别与AB、BC交于点
题目详情
如图,边长为4的正方形ABCD内接于点O,点E是
上的一动点(不与A、B重合),点F是
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
①
=
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+
.
其中正确的是___(把你认为正确结论的序号都填上).
 |
| AB |
 |
| BC |
①
 |
| AE |
 |
| BF |
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+
| | 2 |
其中正确的是___(把你认为正确结论的序号都填上).

▼优质解答
答案和解析
①如图所示,
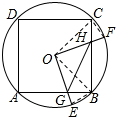
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
,
∴△BOE≌△COF,
∴BE=CF,
∴
=
,①正确;
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,
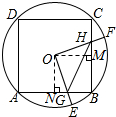
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=
=
,
∴其最小值为2
,D错误.
故答案为:①②.

∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,
|
∴△BOE≌△COF,
∴BE=CF,
∴
 |
| AE |
 |
| BF |
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,

∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=
| BG2+BH2 |
| x2+(4-x)2 |
∴其最小值为2
| 2 |
故答案为:①②.
看了 如图,边长为4的正方形ABC...的网友还看了以下:
关于力的分解问题物体A B经无摩擦的定滑轮用细线连在一起,A物体受水平向右的力F的作用,此时B匀速 2020-05-17 …
蹄形磁铁上方放置一通有方向如图电流I的轻质直导线ab,则ab运动的情况是()A.a端转向纸外,b端 2020-07-05 …
大学物理问题一皮带传动装备,A、B两轮上套有皮带,外力距M作用在A轮上是其转动,并通过皮带带动B. 2020-07-22 …
如图所示,A、B两物体在同一点开始运动,从A、B两物体的位移图线可知下述说法中正确的是()A.A、B 2020-11-03 …
一元二次解答代数式已知实数a.b满足a^2+3a+1=0,b^2+3b+1=o,求b/a+/b的值 2020-11-18 …
如图,M是定滑轮,N是动滑轮,A和B是两个重物.设细绳和滑轮质量及摩擦均不计,整个系统处于静止状态. 2020-11-28 …
某司机再一次车祸中受重伤,急需输血,经化验,他的血型是AB型,正常情况下应给他输入的血液为()A.O 2020-12-18 …
小林同学不幸在车祸中受伤,失血过多,急需输血,经化验,他的血型是A型.下面最适合给小林输血的血型是( 2020-12-24 …
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、B、C、D的坐标分别为A(9, 2020-12-25 …
如图,在平面直角坐标系中,点A(-6,0)、点C(0,4),四边形OABC是矩形,以点O为圆心的⊙O 2020-12-25 …