早教吧作业答案频道 -->数学-->
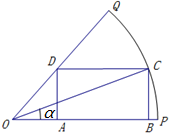
如图,已知OPQ是半径为1,圆心角为π3的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.(1)求扇形OPQ的面积;(2)记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大
题目详情
如图,已知OPQ是半径为1,圆心角为
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.
(1)求扇形OPQ的面积;
(2)记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
| π |
| 3 |

(1)求扇形OPQ的面积;
(2)记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
▼优质解答
答案和解析
(1)扇形OPQ的面积=
•
•1•1=
;
(2)在RT△OBC中,OB=OC•cosα=cosα,BC=OC•sinα=sinα
在RT△OAD中,OA=
sinα,AB=OB-OA=cosα-
sinα
矩形ABCD的面积S=AB•BC=(cosα-
sinα)sinα=
sin(2α+
)-
由0<α<
,得
<2α+
<
所以当2α+
=
即α=
时,矩形ABCD的面积最大,最大面积为
.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
(2)在RT△OBC中,OB=OC•cosα=cosα,BC=OC•sinα=sinα
在RT△OAD中,OA=
| ||
| 3 |
| ||
| 3 |
矩形ABCD的面积S=AB•BC=(cosα-
| ||
| 3 |
| ||
| 3 |
| π |
| 6 |
| ||
| 6 |
由0<α<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
所以当2α+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| ||
| 6 |
看了 如图,已知OPQ是半径为1,...的网友还看了以下:
已知三角形ABC,角A,B,C对应三边分别为a,b,c.已知cosA=2/3,sinB=根号5co 2020-04-05 …
如图,D是等腰Rt△ABC的直角边BC上一点,AD的垂直平分线EF分别交AB,AC于点E,F,BC 2020-04-26 …
已知关于x的二次函数y=ax2和y=bx2.开口大小相同,方向相反,形状相同.求a为什么a=-2呀 2020-05-13 …
三角形A.B.C的对边为a.b.c.已知cosA=2/3.sinB=√5cosC.求tanC的值. 2020-05-15 …
在三角形ABC中,a、b、c分别是A、B、C的对边,且b2+c2=a2+bc.若a=2,求三角形周 2020-07-09 …
在三角形ABC中,A,B,C,所对的边a,b,c满足cosC=1-8b^2/a^2,求1/TANA 2020-07-21 …
在三角形ABC中,内角A,B,C所对的边为abc已知cosA=2/3.sinB=√5cos在三角形 2020-07-21 …
已知椭圆x^2/a^2+Y^2/b^2=1(a>b>0)的离心率根号2/2,且经过点(2,根号2) 2020-08-01 …
5月12日的问答中一题:锐角三角形ABC中,角A、B、C的对边分别为a、b、c,且b=2asinB 2020-08-02 …
已知m=(2cosx2根号3sinx,1),n=(cosx,-y),满足mn=0(1)将y表示为x的 2020-11-01 …