在坐标平面内，如果一个凸四边形的两条对角线分别平行于坐标轴，且有一条对角线恰好平分另一条对角线，则把这样的凸四边形称为坐标平面内的“箏状四边形”．（1）已知箏状四边形ABC

Question

在坐标平面内，如果一个凸四边形的两条对角线分别平行于坐标轴，且有一条对角线恰好平分另一条对角线，则把这样的凸四边形称为坐标平面内的“箏状四边形”．
（1）已知箏状四边形ABCD的三个顶点坐标为A（3，2），B（5，1），C（8，2），则顶点D的坐标为多少．
（2）如果箏状四边形ABCD的三个顶点坐标为A（-6，-3），B（-4，-6），C（-2，-3），则顶点D纵坐标y的取值范围为多少．
（3）已知面积为30的箏状四边形ABCD相邻两个顶点的坐标分别为A（3，1），B（6，3），其中一条对角线长为6，M，N分别是AB，BC的中点，P为对角线上一动点，连结MN，MP，NP，试求△MNP周长的最小值．

Answer 1

（1）如图1中，

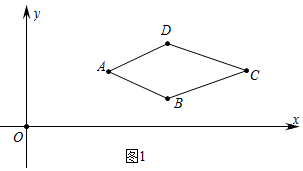
由题意AC垂直平分线段线段BD，可知B、D关于直线AC对称，
∵A（3，2），B（5，1），C（8，2），
∴D（5，3）．

（2）如图2中，

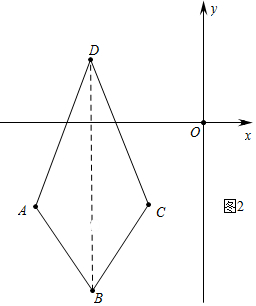
由题意可知，BD垂直平分线段AC，
∵四边形ABCD是凸四边形，A（-6，-3），B（-4，-6），C（-2，-3），
∴顶点D纵坐标y的取值范围：y>-3．

（3）如图3中，

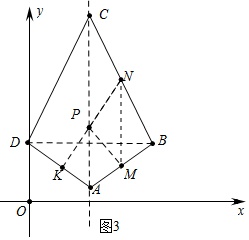
①当点P在对角线AC上时，作点M关于AC的对称点K，连接KN交AC于点P，此时△PMN的周长最小．
由题意A（3，1），B（6，3），
∵对角线BD=6，
∴D（0，3），
∵(1)/(2)×6×AC=30，
∴AC=10，
∴C（3，11），
∴M（4.5，2），N（4.5，7），K（1.5，2）
∴MN=5，KN=√(32+52)=√(34)，
△PMN的周长的最小值为√(34)+5．
②当点P在对角线BD上时，△PMN的周长的最小值不存在．
∴△PMN的周长的最小值问题√(34)+5．