早教吧作业答案频道 -->数学-->
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=-x+b与x轴交于点B.(1)b的值为;(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:
题目详情
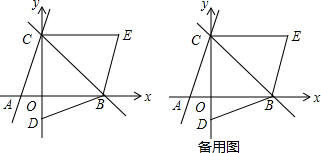
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=-x+b与x轴交于点B.
(1)b的值为___;
(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1)b的值为___;
(2)若点D的坐标为(0,-1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.

▼优质解答
答案和解析
(1)∵直线y=3x+3与x轴交于点A,与y轴交于点C,
∴C(0,3),
∵过点C的直线y=-x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=-x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=-1,
∴A(-1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形.
(3) 存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
方法①如图,
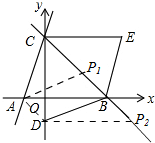
∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,-m+3),
∴PB2=(m-3)2+(-m+3)2,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴PB2=AD2,
∵AD2=2,
∴(m-3)2+(-m+3)2=2.
∴m1=2,m2=4,
∴P(2,1)或P(4,-1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
方法②∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),
∴过点B的直线l∥AD,直线l解析式为y=-x+3,
∴D(0,-1),
∴过点D的直线l'∥AB,直线l'的解析式为y=-1,
∴直线l和l'的交点坐标为M(4,-1),
∵直线BC解析式为y=-x+3.
∴点M在直线BC上,即点M就是所找的点P,
∴P(4,-1),
∵D(0,-1),B(3,0),
∴直线BD的解析式为y=
x-1,
∴过点A的直线a∥BD,直线a的解析式为y=
x+
,
∵直线l解析式为y=-x+3,
∴直线l和直线a的交点坐标为N(2,1),
∵直线BC解析式为y=-x+3.
∴点N在直线BC上,即点N就是所找的点P,
∴P(2,1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
∴C(0,3),
∵过点C的直线y=-x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=-x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=-1,
∴A(-1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形.
(3) 存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
方法①如图,

∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=-x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,-m+3),
∴PB2=(m-3)2+(-m+3)2,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴PB2=AD2,
∵AD2=2,
∴(m-3)2+(-m+3)2=2.
∴m1=2,m2=4,
∴P(2,1)或P(4,-1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
方法②∵A(-1,0)、D(0,-1),
∴直线AD解析式为y=-x-1,
∵B(3,0),
∴过点B的直线l∥AD,直线l解析式为y=-x+3,
∴D(0,-1),
∴过点D的直线l'∥AB,直线l'的解析式为y=-1,
∴直线l和l'的交点坐标为M(4,-1),
∵直线BC解析式为y=-x+3.
∴点M在直线BC上,即点M就是所找的点P,
∴P(4,-1),
∵D(0,-1),B(3,0),
∴直线BD的解析式为y=
| 1 |
| 3 |
∴过点A的直线a∥BD,直线a的解析式为y=
| 1 |
| 3 |
| 1 |
| 3 |
∵直线l解析式为y=-x+3,
∴直线l和直线a的交点坐标为N(2,1),
∵直线BC解析式为y=-x+3.
∴点N在直线BC上,即点N就是所找的点P,
∴P(2,1),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.点P的坐标为P1(2,1)或P2(4,-1).
看了 如图,已知直线y=3x+3与...的网友还看了以下:
如图,已知正方形ABCD的边长是1,E为CD的中点,P为正方形边上的一个动点,动点P从A出发沿A⇒ 2020-05-13 …
①已知a小于c小于0b大于0且a的绝对值大于b的绝对值大于c的绝对值则a的绝对值+b的绝对值-c的 2020-05-14 …
已知有理数A大于有理数B,则下列说法正确的是( ).A.A的绝对值大于B的绝对值.B.A的绝对值小 2020-05-16 …
初一数学!擅长的请进!一、利用a的绝对值和b的绝对值表示a+b的结果1、a大于0,b小于0,a的绝 2020-07-02 …
我记不清楚杂答这类型的题咯有理数A小于0,B大于0A的绝对值小于B的绝对值简化A-B的绝对值-A+ 2020-07-15 …
如果a大于b,则下列不等式成立的是A,ab大于0B,a-b大于0C,绝对值a大于绝对值b如果a大于 2020-08-03 …
下列对M区的分析正确的是()A.若a值大于b值,M区可能为高岗地B.若a值小于b值,M区可能为井灌区 2020-11-20 …
help!1、已知a小于负一,负一小于等于c小于等于零,a小于b小于c,则abc和的绝对值减去b减c 2020-12-17 …
读太阳直射点周年变化示意图.完成8-10题.当太阳直射点位于D点时()A.地中海沿岸正值雨季B.非洲 2020-12-27 …
如果a,b分别表示两个有理数,若绝对值a小于b,那么下列各判断中正确的是A若绝对值a小于b,则a小于 2021-02-02 …