早教吧作业答案频道 -->数学-->
已知∠MAN=135°,正方形ABCD绕点A旋转.(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.①如图1,若BM=DN,则线段MN与BM+DN
题目详情
已知∠MAN=135°,正方形ABCD绕点A旋转.
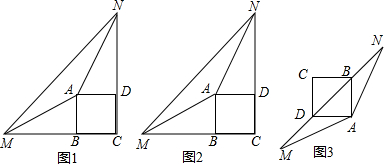
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是___
②如图2,若BM≠DN,请判断①中的数量关系关系是否仍成立?并说明理由.
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM、AN分别与直线BD交于点M、N,探究:以线段BM、DN的长度为三边长的三角形是何种三角形?并说明理由.

(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是___
②如图2,若BM≠DN,请判断①中的数量关系关系是否仍成立?并说明理由.
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM、AN分别与直线BD交于点M、N,探究:以线段BM、DN的长度为三边长的三角形是何种三角形?并说明理由.
▼优质解答
答案和解析
(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:
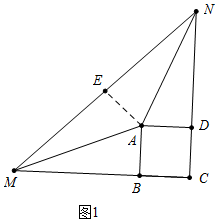
在△ADN与△ABM中,
,
∴△ADN≌△ABM(SAS),
∴AN=AM,∠NAD=∠MAB,
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=
(360°-135°-90°)=67.5°,
作AE⊥MN于E,则MN=2NE,∠NAE=
∠MAN=67.5°.
在△ADN与△AEN中,
,
∴△ADN≌△AEN(AAS),
∴DN=EN,
∵BM=DN,MN=2EN,
∴MN=BM+DN.
故答案为MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
将△ABM绕点A逆时针旋转90°得到△ADE,易知N、D、E三点共线.
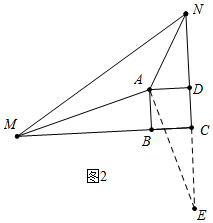
∵AM=AP,∠MAE=90°
∴∠EAN=360°-∠MAN-∠MAE=360°-135°-90°=135°,
∴∠MAN=∠NAE,
在△ANM与△ANP中,
,
∴△ANM≌△ANE(SAS),
∴MN=EN,
∵EN=DE+DN=BM+DN,
∴MN=BM+DN;
(2)结论:以线段BM、DN的长度为三边长的三角形是直角三角形.
理由:将△ABM绕点A逆时针旋转90°得到△ADE,连接NE,
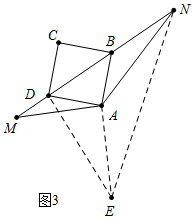
∵∠MAE=90°,∠MAN=135°,
∴∠NAE=360°-∠MAN-∠MAE=135°
∴∠EAN=∠MAN,
∵AM=AE,AN=AN,
∴△AMN≌△AEN,
∴MN=EN,
∵∠ADE=∠ABM=∠BDA=45°,
∴∠BDE=∠BDA+∠ADE=90°
∴DN2+DE2=NE2,∵BM=DE,MN=EN,
∴DN2+BM2=MN2
∴以线段BM、MN、DN的长度为三边长的三角形是直角三角形.

在△ADN与△ABM中,
|
∴△ADN≌△ABM(SAS),
∴AN=AM,∠NAD=∠MAB,
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=
| 1 |
| 2 |
作AE⊥MN于E,则MN=2NE,∠NAE=
| 1 |
| 2 |
在△ADN与△AEN中,
|
∴△ADN≌△AEN(AAS),
∴DN=EN,
∵BM=DN,MN=2EN,
∴MN=BM+DN.
故答案为MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
将△ABM绕点A逆时针旋转90°得到△ADE,易知N、D、E三点共线.

∵AM=AP,∠MAE=90°
∴∠EAN=360°-∠MAN-∠MAE=360°-135°-90°=135°,
∴∠MAN=∠NAE,
在△ANM与△ANP中,
|
∴△ANM≌△ANE(SAS),
∴MN=EN,
∵EN=DE+DN=BM+DN,
∴MN=BM+DN;
(2)结论:以线段BM、DN的长度为三边长的三角形是直角三角形.
理由:将△ABM绕点A逆时针旋转90°得到△ADE,连接NE,

∵∠MAE=90°,∠MAN=135°,
∴∠NAE=360°-∠MAN-∠MAE=135°
∴∠EAN=∠MAN,
∵AM=AE,AN=AN,
∴△AMN≌△AEN,
∴MN=EN,
∵∠ADE=∠ABM=∠BDA=45°,
∴∠BDE=∠BDA+∠ADE=90°
∴DN2+DE2=NE2,∵BM=DE,MN=EN,
∴DN2+BM2=MN2
∴以线段BM、MN、DN的长度为三边长的三角形是直角三角形.
看了 已知∠MAN=135°,正方...的网友还看了以下:
如图,直线a垂直直线b,试作线段MN分别关于a、b成轴对称的线段M’N’和M”N”,并说如图,直线 2020-04-26 …
1.已知线段AB=100毫米,点M在AB上,MB=52毫米,P是AM的中点,求MP的长2.AB=2 2020-05-13 …
一辆质量为2t上网小轿车,驶过半径R=90的一段圆弧形桥面,重力加速度g=10m/s2,求1 若桥 2020-05-17 …
一辆质量m=2t的小轿车,驶过半径r=100m的一段圆弧形桥面,重力加速度g=10m/s2求 .若 2020-05-17 …
一道数学几何中考题在等腰梯形ABCD中,AD平行于BC,AB=CD,AD=3,BC=9,tan角A 2020-07-20 …
已知一个角和这个角的平分线及这个角对边上的高,求作三角形已知:线段M,H和∠α求作:三角形ABC, 2020-08-02 …
如图1,正方形ABCD和正方形QMNP,∠M=∠B,M是正方形ABCD的对称中心,MN交AB于F, 2020-08-02 …
如图所示,线段m的两个端点分别是梯形两个腰从上至下的2,3,4,…n等分点,梯形的两底长为a,b, 2020-08-02 …
1.已知线段AB=6厘米,点C在直线AB上,且BC=2厘米,M为线段AC的中点,求线段AM的长.2. 2020-11-21 …
M河段与N河段降水量的差异和主要原因分别是()A.M河段大于N河段M受西风影响,降水多B.M河段大于 2020-12-27 …