早教吧作业答案频道 -->数学-->
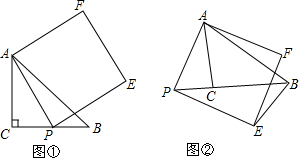
已知△ACB为等腰直角三角形,点P在BC上,以AP为边长作正方形APEF.(1)如图①,当点P在BC上时,求∠EBP;(2)如图②,当点P在BC的延长线上时,求∠EBP.
题目详情
已知△ACB为等腰直角三角形,点P在BC上,以AP为边长作正方形APEF.
(1)如图①,当点P在BC上时,求∠EBP;
(2)如图②,当点P在BC的延长线上时,求∠EBP.
(1)如图①,当点P在BC上时,求∠EBP;
(2)如图②,当点P在BC的延长线上时,求∠EBP.

▼优质解答
答案和解析
(1)如图,
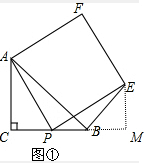
过E作CB垂线,交延长线于点M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
,
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°,
∴∠EBP=135°.
(2)如图,
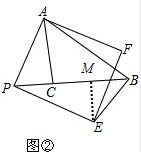
作EM⊥CB,垂足为M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
,
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°.

过E作CB垂线,交延长线于点M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
|
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°,
∴∠EBP=135°.
(2)如图,

作EM⊥CB,垂足为M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
|
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°.
看了 已知△ACB为等腰直角三角形...的网友还看了以下:
关于轨迹的数学题已知点A(0,1),定直线L:y=-1,B为L上的一个动点.过B作直线m垂直于L, 2020-04-25 …
质量为m的木块放在弹簧上,弹簧在竖直方向作简谐振动,当振幅为A时,物体对弹簧压力的最大值是物体重量 2020-06-03 …
说明文中常用的说明方法是A.议论拟人列数字下定义分类别打比方B.作比较抒情插叙引用排比反问C.打比 2020-06-13 …
一电荷Q在某一匀强磁场中沿垂直方向作圆周运动,判断下面几种说法是否正确,并说明理由.A只要速度大小 2020-07-01 …
一物体放在活塞上,活塞以1.0s的周期在竖直方向作谐振动.试问:(1)在多大振幅时,物体与活塞分( 2020-07-12 …
如图,已知点A(63,0),B(0,6),经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动 2020-07-22 …
正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B 2020-07-22 …
已知双曲线x^2/a^2-y^2/b^2=1的离心率e=2√3/3,过点A(a,0)B(0,-b) 2020-07-25 …
如图,直线y=x与直线y=2x-1相交于点B,过B作BA⊥y轴于点A,点A关于点B的对称点为A1, 2020-07-31 …
已知椭圆方程为B(2,0)过点B作直线l与椭圆交与E、F两点,求三角形OBE与三角形OBF的面积比已 2020-11-27 …