早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).(1)求线段AB的长;(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;(3)在(2)的条件下,过点O作OM⊥
题目详情
如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).
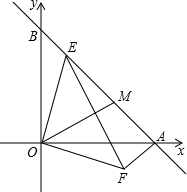
(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;
(3)在(2)的条件下,过点O作OM⊥EF,交AB于点M,试确定线段BE、EM、AM的数量关系?并证明你的结论.

(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;
(3)在(2)的条件下,过点O作OM⊥EF,交AB于点M,试确定线段BE、EM、AM的数量关系?并证明你的结论.
▼优质解答
答案和解析
(1)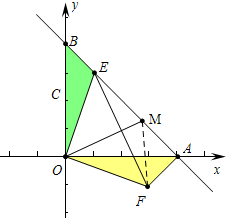 在RT△ABO中,∵AO=OB=4,
在RT△ABO中,∵AO=OB=4,
∴AB=
=
=4
.
(2)∵∠BOA=∠EOF=90°,
∴∠BOE=∠AOF,
在△BOE和△AOF中,
,
∴△BOE≌△AOF,
∴AF=BE,
∴AE+AF=AE+EB=AB=4
.
(3)结论:FM2=AM2+AF2,理由如下:
连接FM.∵OE=OF,OM⊥EF,
∴OM垂直平分分EF,
∴ME=MF,
∵OA=OB,∠AOB=90°,
∴∠OBA=∠OAB=45°
由(1)可知△BOE≌△AOF,
∴BE=AF,∠OBE=∠OAF=45°,
∴∠MAF=∠OAF+∠OAB=90°,
∴FM2=AM2+AF2,
∴EM2=BE2+AM2.
 在RT△ABO中,∵AO=OB=4,
在RT△ABO中,∵AO=OB=4,∴AB=
| AO2+OB2 |
| 42+42 |
| 2 |
(2)∵∠BOA=∠EOF=90°,
∴∠BOE=∠AOF,
在△BOE和△AOF中,
|
∴△BOE≌△AOF,
∴AF=BE,
∴AE+AF=AE+EB=AB=4
| 2 |
(3)结论:FM2=AM2+AF2,理由如下:
连接FM.∵OE=OF,OM⊥EF,
∴OM垂直平分分EF,
∴ME=MF,
∵OA=OB,∠AOB=90°,
∴∠OBA=∠OAB=45°
由(1)可知△BOE≌△AOF,
∴BE=AF,∠OBE=∠OAF=45°,
∴∠MAF=∠OAF+∠OAB=90°,
∴FM2=AM2+AF2,
∴EM2=BE2+AM2.
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
请找出每组字母中与众不同的一个,并将其写在横线上.1.a,l,h,k2.i,b,p,t3.f,n, 2020-05-14 …
解关于x的不等式x的平方-x-a(a-1)>0,用高一上知识x^2-x-a(a-1)>0x^2+[ 2020-05-23 …
在平面直角坐标系中有一点a(a-3,2a-8),点a在横轴上1,a=(),点a在纵轴上,a( 2020-05-24 …
求证:(1)A(n+1,n+1)-A(n,n)=n^2A(n-1,n-1);(2)C(m,n+1) 2020-06-03 …
已知点P的坐标为(a-1,a-5).(1)若点P在x轴上,则a=;(2)若点P在y轴上,则a=;已 2020-06-14 …
计算(a-1)(a+1)(a2+1)(a上+1)的过程为:原式=(a2-1)(a2+1)(a上+1 2020-07-09 …
1.(A∩B)右上角标个C是什么意思?其中A,B,C都是任意三个集合.2.x∈A∩B中∈号上1.( 2020-07-30 …
函数题,二十分已知函数f(x)=x的三次方加上ax的平方加上x加上1.a属于R.(1)讨论函数f( 2020-08-01 …
若a>1,则a+(1/a-1)的最小值a加上1/a-1 2020-08-01 …
我有很多英语难题要各位大哥哥、姐姐帮帮忙!1.改错(在括号里写出有错的单词的序号如:(A)或(B)并 2020-10-30 …