早教吧作业答案频道 -->数学-->
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.(1)在图1中,∠AOC=,∠BOC=.(2)将
题目详情
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
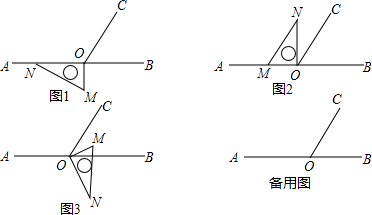
(1)在图1中,∠AOC=___,∠BOC=___.
(2)将图1中的三角板按图2的位置放置,使得OM在射线OA上,则∠CON=___;
(3)将上述直角三角板按图3的位置放置,使得OM在∠BOC的内部,求∠BON-∠COM的度数.

(1)在图1中,∠AOC=___,∠BOC=___.
(2)将图1中的三角板按图2的位置放置,使得OM在射线OA上,则∠CON=___;
(3)将上述直角三角板按图3的位置放置,使得OM在∠BOC的内部,求∠BON-∠COM的度数.
▼优质解答
答案和解析
(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
看了 如图1,点O为直线AB上一点...的网友还看了以下:
关于求逆的.设方阵A满足方程A的平方-A-2E=O(opq的o欧),证明:A及A+2E均可逆,并求 2020-04-27 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
第二次 makefile 提示 make:`myapp' is up to date,myapp 2020-05-16 …
∵EM是⊙O的切线,怎么推出EB•EC=EM2①?,看题后回答.(2005•温州)如图,已知四边形 2020-05-21 …
找出发音相同的单词opposite中第二个o发音相同的是:A.c[o]mpanion[kəmˈpæ 2020-06-06 …
A/O排泥问题:arm:A/O后面有个沉淀池.排泥是只排沉淀池的泥么?如果是这样,想保证A/O的泥 2020-07-07 …
等边三角形ABC,AB=a,O为三角形的中心,过O点的直线交AB于M,交AC于N,求1.等边三角形 2020-08-03 …
大气臭氧层的反应是:O+O3=2O2△H,该反应的能量变化如图所示,下列叙述中,正确的是()A.O+ 2020-10-31 …
()()a()()()()a()()()()a()()()()()a()()()()()()a()( 2020-11-07 …
已知:如图,直线与x轴相交于点A,与直线相交于点P(2,).(1)请判断的形状并说明理由.(2)动点 2020-12-15 …