现有半径为R、圆心角（∠AOB）为90°的扇形材料，要裁剪出一个五边形工件OECDF，如图所示．其中E，F分别在OA，OB上，C，D在AB上，且OE=OF，EC=FD，∠ECD=∠CDF=90°．记∠COD=2θ，五边形OECDF的面积

Question

现有半径为R、圆心角（∠AOB）为90°的扇形材料，要裁剪出一个五边形工件OECDF，如图所示．其中E，F分别在OA，OB上，C，D在

AB

上，且OE=OF，EC=FD，∠ECD=∠CDF=90°．记∠COD=2θ，五边形OECDF的面积为S．

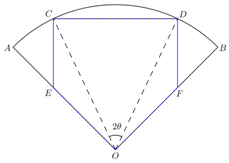
（1）试求S关于θ的函数关系式；
（2）求S的最大值．

Answer 1

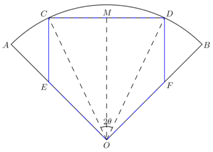（1）设M是CD中点，连OM，由OC=OD，可知OM⊥CD，
∠COM=∠DOM=，(1)/(2)∠COD=θ，MD=Rsinθ，
又OE=OF，EC=FD，OC=OD，可得△CEO≌△DFO，
故∠EOC=∠DOF，可知∠AOM=∠BOM=(1)/(2)∠AOB=(π)/(4)，…（2分）
又DF⊥CD，OM⊥CD，所以MO∥DF，故∠DFO=(3π)/(4)，
在△DFO中，有(DF)/(sin∠DOF)=(DO)/(sin∠DFO)，
可得DF=(Rsin((π)/(4)-θ))/(sin(3π)/(4))=R(cosθ-sinθ)…（5分）
所以S=S_△COD+S_ODF+S_OCE=S_△COD+2S_ODF=(1)/(2)R2sin2θ+Rsinθ(Rcosθ-Rsinθ)
=R2sin2θ-R2sin2θ(0<θ<(π)/(4))…（8分）
（2）S=R2sin2θ-(1)/(2)R2(1-cos2θ)=R2(sin2θ+(1)/(2)cos2θ)-(1)/(2)R2…（10分）
=(√(5))/(2)R2sin(2θ+φ)-(1)/(2)R2（其中φ=arctan(1)/(2)）                  …（12分）
当2θ+φ=(π)/(2)，即θ=(π)/(4)-(φ)/(2)时，sin（2θ+φ）取最大值1．
又(π)/(4)-(φ)/(2)∈(0，(π)/(4))，所以S的最大值为(√(5)-1)/(2)R2．                   …（14分）