早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,等边△OAB的边OB在y轴上,点A的坐标为(1,3).(1)线段OA的长为;(2)①如图1,若C为OB上一点,以AC为边在右侧作等边△
题目详情
如图,在平面直角坐标系xOy中,等边△OAB的边OB在y轴上,点A的坐标为(1,
).
(1)线段OA的长为___;
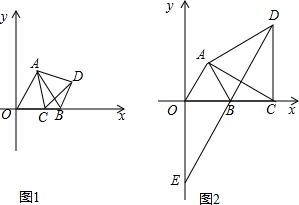
(2)①如图1,若C为OB上一点,以AC为边在右侧作等边△ACD,连接BD,求证;OA∥BD.
②如图2,若C为OB延长线上一点,则OA∥BD还成立吗?若成立,请证明;若不成立,请说明理由.
(3)如图2,延长DB交y轴于点E,若BD=BE,求点C的坐标.
| | 3 |
(1)线段OA的长为___;
(2)①如图1,若C为OB上一点,以AC为边在右侧作等边△ACD,连接BD,求证;OA∥BD.
②如图2,若C为OB延长线上一点,则OA∥BD还成立吗?若成立,请证明;若不成立,请说明理由.
(3)如图2,延长DB交y轴于点E,若BD=BE,求点C的坐标.

▼优质解答
答案和解析
(1)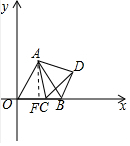 作AF⊥OB于F,
作AF⊥OB于F,
∵点A的坐标为(1,
),
∴OF=1,AF=
,
由勾股定理得,OA=
=2,
故答案为:2;
(2)①∵△OAB和△ACD都是等边三角形,
∴∠OAB=∠CAD=60°,
∴∠OAC=∠BAD,
在△OAC和△BAD中,
,
∴△OAC≌△BAD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠OBA+∠ABD=120°,又∠OAB=60°,
∴OA∥BD;
②∵△OAB和△ACD都是等边三角形,
∴∠OAB=∠CAD=60°,
∴∠OAC=∠BAD,
同理,△OAC≌△BAD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠OBA+∠ABD=120°,又∠OAB=60°,
∴OA∥BD;
(3)在△EOB和△DAB中,
,
∴△EOB≌△DAB,
∴∠ADB=∠OEB=30°,
∴∠CDB=30°,
∴OE∥CD,又BD=BE,
∴OC=2OB=4,
则点C的坐标为(4,0).
 作AF⊥OB于F,
作AF⊥OB于F,∵点A的坐标为(1,
| 3 |
∴OF=1,AF=
| 3 |
由勾股定理得,OA=
| OF2+AF2 |
故答案为:2;
(2)①∵△OAB和△ACD都是等边三角形,
∴∠OAB=∠CAD=60°,
∴∠OAC=∠BAD,
在△OAC和△BAD中,
|
∴△OAC≌△BAD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠OBA+∠ABD=120°,又∠OAB=60°,
∴OA∥BD;
②∵△OAB和△ACD都是等边三角形,
∴∠OAB=∠CAD=60°,
∴∠OAC=∠BAD,
同理,△OAC≌△BAD,
∴∠ABD=∠AOC=60°,
∴∠OBD=∠OBA+∠ABD=120°,又∠OAB=60°,
∴OA∥BD;
(3)在△EOB和△DAB中,
|
∴△EOB≌△DAB,
∴∠ADB=∠OEB=30°,
∴∠CDB=30°,
∴OE∥CD,又BD=BE,
∴OC=2OB=4,
则点C的坐标为(4,0).
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
一根长绳,先用了全长的5分之1,又用去了全长的4分之1,后用去的比先用去的长1米,这根长多少米.算式 2020-03-30 …
把一根竹竿竖直插入水中,在浸湿处涂上红点,将竹竿插入水中两次,第一次浸湿部分占竹竿总长3分之2第二 2020-04-25 …
如图,已知Rt△ABC中,∠ACB=90°,∠A=15°,CD是边AB上的高,点E在边AB或AB的 2020-05-14 …
把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.(1)求AD的长;( 2020-05-16 …
有两根绳子,长的必短的长1倍.现在把每根绳子都剪掉6分米,发现长的一根比短的一根长2倍.问:这两根 2020-06-26 …
已知三角形的周长为50,第一条边长为5m+2n,第二条边长的2倍比第一条边长少2m-n+1,求每三 2020-07-02 …
滑雪板可以轻易在雪地上滑行,是由于,若滑雪者与滑雪板总重为720N,每块滑雪板的长1.5m、宽0. 2020-07-21 …
笑笑在本子上画自己卧室的平面图,她用8厘米表示自己卧室的长(1)图上1厘米表示的实际距离是多少厘米 2020-07-28 …
有一个四棱锥,其正视图和侧视图都是直角三角形.直角边为1和2,俯视图为边长1的正方形,如图所示,求 2020-08-01 …
C点是长为19cm的线段AB上的一点,根据下列条件求AC.BC的长1.AC是BC的两倍2.AC:B 2020-08-02 …