早教吧作业答案频道 -->数学-->
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.(1)求证:DE是⊙O的切线;(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
题目详情
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
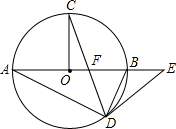
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.

(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
▼优质解答
答案和解析
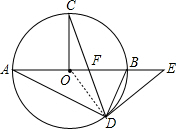 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,
∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2) ∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED=∠DAE,
∴△EBD∽△EDA,
∴
=
,即
=
,
∴x=2,
∴BE=2.
 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2) ∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED=∠DAE,
∴△EBD∽△EDA,
∴
| DE |
| AE |
| BE |
| DE |
| x+2 |
| 6+2 |
| x |
| x+2 |
∴x=2,
∴BE=2.
看了 如图,在⊙O中,AB为直径,...的网友还看了以下:
半圆O的直径AB=12,半径OC⊥AB,⊙O‘与半圆O相内切,并且与OB,OC相切于点D,F.求⊙ 2020-06-06 …
如图,AB为圆O的直径,PB为O的切线,AC//OP,点C在圆O上,OP交圆O于D,DA交BC于G 2020-06-27 …
如图,AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,BC=3,CD=2AB是⊙O的直径 2020-07-21 …
如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心 2020-07-22 …
如图,在圆心O中,AO是半径,ABAC是弦,弧AB=弧AC,点O在直角BAC的平分线上吗?为什么? 2020-07-29 …
数学圆的切线1.如图,在三角形ABC中,角BCA=90度,角A=30度,以AB为直径画圆O,延长A 2020-07-31 …
已知AB是半径为6的⊙O的直径,点C是⊙O的半径OA上的动点,PC⊥AB交⊙O于E,交OA于C,P 2020-07-31 …
如图,在O中,半径OA⊥OB,过点OA的中点C作FD∥OB交O于D、F两点,且CD=3,以O为圆心, 2020-11-26 …
已知:AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠DOE=60º.求∠C 2020-11-27 …
那新疆2013中考数学的23题呢?刚刚问的是24题,如图,已知⊙O的半径为4,CD是⊙O的直径,AC 2021-01-22 …