早教吧作业答案频道 -->数学-->
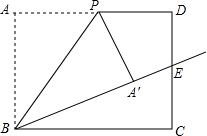
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为.
题目详情
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为___.

▼优质解答
答案和解析
∵四边形ABCD是矩形,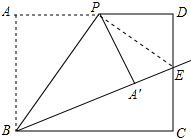
∴AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,
∵E是CD的中点,
∴DE=CE=5,
∴BE=
=
=13,
由折叠的性质得:∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,
∴∠PA′E=90°,A′E=13-10=3,
连接PE,如图所示:
设PA′=PA=x,则PD=12-x,
由勾股定理得:PE2=PA′2+A′E2=PD2+DE2,
即x2+32=(12-x)2+52,
解得:x=
,
∴PA′=
,PD=12-
=
,
∴四边形DPA′E的面积=
×3×
+
×5×
=
;
故答案为:
.

∴AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,
∵E是CD的中点,
∴DE=CE=5,
∴BE=
| BC2+CE2 |
| 122+52 |
由折叠的性质得:∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,
∴∠PA′E=90°,A′E=13-10=3,
连接PE,如图所示:
设PA′=PA=x,则PD=12-x,
由勾股定理得:PE2=PA′2+A′E2=PD2+DE2,
即x2+32=(12-x)2+52,
解得:x=
| 20 |
| 3 |
∴PA′=
| 20 |
| 3 |
| 20 |
| 3 |
| 16 |
| 3 |
∴四边形DPA′E的面积=
| 1 |
| 2 |
| 20 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
| 70 |
| 3 |
故答案为:
| 70 |
| 3 |
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
1.A、B、C、D、E五位男生参加比赛,四位旁观者作如下预测:旁观者一:E将取得第三名,A将取得第 2020-05-13 …
编写一个加密程序,要求:对于字母,将A换成D,将B换成E,…,将Y换成B,将Z换成C;将a换成d, 2020-05-13 …
如图,有一只老鼠沿着平行四边形A→B→C——D的方向逃跑,同时有一只猫也从点A出发沿A→B→C—— 2020-05-17 …
给句中的"临"选择正确的意思.A.到;来.B.靠近;对着.C.将要;快要.D.封建皇帝上朝.E.照 2020-05-23 …
已知直线y=-4分之3x+6的图像交x轴与点A,交y轴于点B,在线段OA上找一点E,将△ABE沿着 2020-06-14 …
有6个门铃按纽,但只有一个是真按纽.有一张告示:A在B的左边;B在C右边的第三个;C在D的右边;D 2020-06-21 …
在评奖会上,A、B、C、D、E、F、G、H竞争一项金奖.由一个专家小组投票,票数最多的将获金奖.如 2020-06-27 …
如图,C、D、E将线段AB分为四部分,且AC:CD:DE:EB=2:3:4:5,M、P、Q、N分别 2020-07-22 …
一道算数题设一个数为A(A为1-9其中一数)A+3-2=BB×9=C将C的个位和十位相加=DD×50 2020-11-23 …
如图,在四边形ABCD中,AD//BC,若沿着BD将△ABDABD折叠则A点恰好落到BC边上的E点处 2021-01-12 …