早教吧作业答案频道 -->数学-->
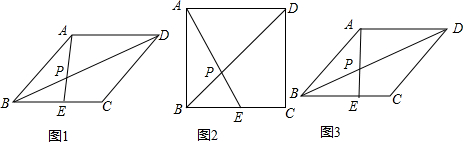
如图1是边长为6的菱形ABCD,E是BC的中点,AE、BD相交于点P.(1)如图2,当∠ABC=90°时,求BP的长.(2)如图3,当∠ABC角度在改变时,BP的中垂线与边BC的交点F的位置是否发生变化?如果不变
题目详情
如图1是边长为6的菱形ABCD,E是BC的中点,AE、BD相交于点P.
(1)如图2,当∠ABC=90°时,求BP的长.
(2)如图3,当∠ABC角度在改变时,BP的中垂线与边BC的交点F的位置是否发生变化?如果不变,请求出BF的长;如果改变,请说明理由.
(3)当∠ABC从90°逐步减少到30°的过程中,求P点经过路线长.
(1)如图2,当∠ABC=90°时,求BP的长.
(2)如图3,当∠ABC角度在改变时,BP的中垂线与边BC的交点F的位置是否发生变化?如果不变,请求出BF的长;如果改变,请说明理由.
(3)当∠ABC从90°逐步减少到30°的过程中,求P点经过路线长.

▼优质解答
答案和解析
(1)∵E是BC的中点,
∴BE=CE=
BC,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∴△BEP∽△DAP,
∴
=
=
,
∵∠ABC=90°,
∴菱形ABCD是正方形,
∴BD=
=6
,
∴BP=
BD=2
;
(2)不发生变化;理由如下:
∵四边形ABCD是菱形,
∴∠ABD=∠CBD,
又∵BP的中垂线与边BC交于点F,
∴BF=PF,
∴∠FBP=∠BPF,∠BPF=∠ABD,
∴PF∥AB∥CD,
∴
=
=
,
∴BF=
BC=2,
即点F的位置不发生改变;
(3)P点经过路线是以F为圆心,BF为半径的圆弧,长度为
=
π.
∴BE=CE=
| 1 |
| 2 |
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∴△BEP∽△DAP,
∴
| BP |
| DP |
| BE |
| AD |
| 1 |
| 2 |
∵∠ABC=90°,
∴菱形ABCD是正方形,
∴BD=
| 62+62 |
| 2 |
∴BP=
| 1 |
| 3 |
| 2 |
(2)不发生变化;理由如下:
∵四边形ABCD是菱形,
∴∠ABD=∠CBD,
又∵BP的中垂线与边BC交于点F,
∴BF=PF,
∴∠FBP=∠BPF,∠BPF=∠ABD,
∴PF∥AB∥CD,
∴
| BF |
| BC |
| BP |
| BD |
| 1 |
| 3 |
∴BF=
| 1 |
| 3 |
即点F的位置不发生改变;
(3)P点经过路线是以F为圆心,BF为半径的圆弧,长度为
| (90-30)π×2 |
| 180 |
| 2 |
| 3 |
看了 如图1是边长为6的菱形ABC...的网友还看了以下:
如图,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/秒的速 2020-05-16 …
如图,在矩形ABCD中,AB=12CM,BC=6CM,点P沿AB边从点A开始想点B以2cm/s的速 2020-05-16 …
已知a>0,设命题p:函数y=a^x为减函数,命题q:当x[1/2,2]时,y=x+1/x>1/a 2020-05-17 …
命题中的“结论”等同于为真命题时的“必要条件”吗?当命题“如果p,则q”经过推理证明断定是真命题时 2020-05-17 …
杂化时,只有当p轨道未填满时,s轨道的电子才会激发上去吗?如果p的三个轨...杂化时,只有当p轨道 2020-06-07 …
如何证明均值定理?均值定理:已知x,y∈R+,x+y=S,x·y=P(1)如果P是定值,那么当且仅 2020-06-16 …
已知在△ABC中,D是AB上一点,P是AC上一点.(1)当D是AB的中点,若APPC=2,证明:B 2020-07-20 …
有关气体的:T、P、V、n之间的关系有具体的公式吗?当P、T相同时,V与n成正比,当T、V相同时, 2020-07-30 …
有关气体的:T、P、V、n之间的关系有具体的公式吗?当P、T相同时,V与n成正比,当T、V相同时, 2020-07-30 …
已知x,,x+y=p,xy=s,有下列命题其中正确命题的序号是A如果s是定值,那么当且仅当x=y时p 2020-12-31 …