如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．给出下列结论：①△BDE∽△DPE；②FPPH=35；③DP2=PH•PB；④tan∠DBE=2-3．其中正确的是

Question

如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．给出下列结论：
①△BDE∽△DPE；②

(FP)/(PH)=(3)/(5)；③DP²=PH•PB；④tan∠DBE=2-√(3)．
其中正确的是（　　）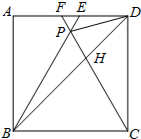

A. ①②③④

B. ①②④

C. ②③④

D. ①③④

Answer 1

∵△BPC是等边三角形，
∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，
在正方形ABCD中，
∵AB=BC=CD，∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°，
∴∠CPD=∠CDP=75°，∴∠PDE=15°，
∵∠PBD=∠PBC-∠HBC=60°-45°=15°，
∴∠EBD=∠EDP，
∵∠DEP=∠DEB，
∴△BDE∽△DPE；故①正确；
∵PC=CD，∠PCD=30°，
∴∠PDC=75°，
∴∠FDP=15°，
∵∠DBA=45°，
∴∠PBD=15°，
∴∠FDP=∠PBD，
∵∠DFP=∠BPC=60°，
∴△DFP∽△BPH，
∴(PF)/(PH)=(DF)/(PB)=(DF)/(CD)=(√(3))/(3)，故②错误；
∵∠PDH=∠PCD=30°，
∵∠DPH=∠DPC，
∴△DPH∽△CDP，
∴(PD)/(CD)=(PH)/(PD)，
∴PD²=PH•CD，
∵PB=CD，
∴PD²=PH•PB，故③正确；
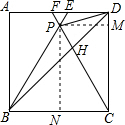
如图，过P作PM⊥CD，PN⊥BC，
设正方形ABCD的边长是4，△BPC为正三角形，
∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，
∴∠PCD=30°
∴CM=PN=PB•sin60°=4×(√(3))/(2)=2√(3)，PM=PC•sin30°=2，
∵DE∥PM，
∴∠EDP=∠DPM，
∴∠DBE=∠DPM，
∴tan∠DBE=tan∠DPM=(DM)/(PM)=(4-2√(3))/(2)=2-√(3)，故④正确；
故答案为：①③④．