早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°)
题目详情
如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
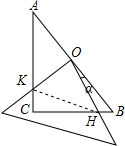
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CKH的面积为
时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.

(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CKH的面积为
| 5 |
| 2 |
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
▼优质解答
答案和解析
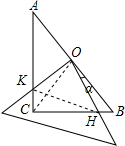 (1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.
(1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.
理由如下:连接OC.
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB,
∴∠OCK=∠B=45°,CO=OB.
又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=α,
在△COK和△BOH中,
,
∴△COK≌△BOH,
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
S△ABC=9.
(2)①由(1)知CK=BH=x,
∵BC=6,
∴CH=6-x,根据题意,得
CH•CK=
,
即(6-x)x=5,解这个方程得x1=1,x2=5,
此两根满足条件:0<x<6,
所以当△CKH的面积为
时,x的取值是1或5;
②设△OKH的面积为S,由(1)知四边形CHOK的面积为9,
∴S△OKH=S四边形CHOK-S△CKH=9-
x(6-x)=
(x2-6x)+9=
(x-3)2+
,
∵
>0,
∴当x=3时,函数S△OKH有最小值
,
∵x=3满足条件0<x<6,
∴△OKH的面积存在最小值,此时x的值是3.
 (1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.
(1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.理由如下:连接OC.
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB,
∴∠OCK=∠B=45°,CO=OB.
又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=α,
在△COK和△BOH中,
|
∴△COK≌△BOH,
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
| 1 |
| 2 |
(2)①由(1)知CK=BH=x,
∵BC=6,
∴CH=6-x,根据题意,得
| 1 |
| 2 |
| 5 |
| 2 |
即(6-x)x=5,解这个方程得x1=1,x2=5,
此两根满足条件:0<x<6,
所以当△CKH的面积为
| 5 |
| 2 |
②设△OKH的面积为S,由(1)知四边形CHOK的面积为9,
∴S△OKH=S四边形CHOK-S△CKH=9-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵
| 1 |
| 2 |
∴当x=3时,函数S△OKH有最小值
| 9 |
| 2 |
∵x=3满足条件0<x<6,
∴△OKH的面积存在最小值,此时x的值是3.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
A ,B ,C 三点为一直角三角形的三个顶点,角B 为30度.现在A 、B两点放置两点电荷Qa、Q 2020-04-05 …
如图为一突触的结构,在a、d两点连接一个灵敏电流计.已知ab=bd,若分别刺激b、c两点,灵敏电流 2020-07-07 …
一条直线上有a,b,c,d四个点,ab=bc=cd,若在b点处放一个负点电荷,则().A.a,c两点 2020-10-31 …
已知△ABC中,∠C=90°,AC=2,BC=3,M为AB中点,1.以C为圆心,2为半径作○C,则点 2020-11-26 …
为了更好地引导和规范慈善行为,促进慈善事业健康发展,我国积极开展慈善立法工作,依法治善。这体现了() 2020-12-09 …
10.01读作A.一零点零一B.一点零零一C.十点一零D.十点零一 2020-12-27 …
如图为一突触的结构,在a、d两点连接一个灵敏电流计.已知ab=bd,若分别刺激b、c两点,灵敏电流计 2020-12-30 …
如图,直线y=-x+3与x轴,y轴分别交于B,C两点,抛物线y=-x²+bx+c经过点B和点C,点A 2021-01-10 …