早教吧作业答案频道 -->数学-->
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.(1)求证:DP⊥平面A1ABB1;(2)求证:PQ∥平面ADD1A1.(3)若E为CC1的中点,能否在CP上找一点F
题目详情
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.
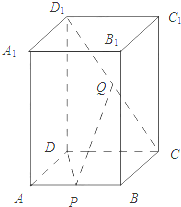
(1)求证:DP⊥平面A1ABB1;
(2)求证:PQ∥平面ADD1A1.
(3)若E为CC1的中点,能否在CP上找一点F,使得EF∥面DPQ?并给出证明过程.

(1)求证:DP⊥平面A1ABB1;
(2)求证:PQ∥平面ADD1A1.
(3)若E为CC1的中点,能否在CP上找一点F,使得EF∥面DPQ?并给出证明过程.
▼优质解答
答案和解析
证明:(1)连结BD
∵在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,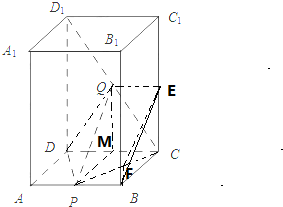
∴AP=AB=BD,
∵P为AB的中点,∴DP⊥AB,
∵AA1⊥平面ABCD,DP⊂平面ABCD,
∴AA1⊥DP,
∵AA1∩AB=A,∴DP⊥平面A1ABB1.
(2)取CD中点M,连结PM、QM,
∵P为AB的中点,Q为CD1的中点,
∴PM∥AD,QM∥DD1,
∵AD∩DD1=D,PM∩QM=M,
AD、DD1⊂平面ADD1,PM、QM⊂平面PQF,
∴平面ADD1∥平面MPQ,
∵PQ⊂平面PQF,∴PQ∥平面ADD1A1.
(3)连结EB,
∵Q为CD1的中点,E是CC1的中点,P为AB中点,∴QE
PB,
∴四边形PBEQ是平行四边形,∴BE∥PQ,
过B作BF∥AD,交PC于F,
∵BE∥PQ,BF∥AD,BE∩BF=B,PQ∩PD=P,
BE、BF⊂平面BEF,PQ、PD⊂平面PDQ,
∴平面BEF∥平面PDQ,
∵EF⊂平面BEF,∴EF∥面DPQ.
∵在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,

∴AP=AB=BD,
∵P为AB的中点,∴DP⊥AB,
∵AA1⊥平面ABCD,DP⊂平面ABCD,
∴AA1⊥DP,
∵AA1∩AB=A,∴DP⊥平面A1ABB1.
(2)取CD中点M,连结PM、QM,
∵P为AB的中点,Q为CD1的中点,
∴PM∥AD,QM∥DD1,
∵AD∩DD1=D,PM∩QM=M,
AD、DD1⊂平面ADD1,PM、QM⊂平面PQF,
∴平面ADD1∥平面MPQ,
∵PQ⊂平面PQF,∴PQ∥平面ADD1A1.
(3)连结EB,
∵Q为CD1的中点,E是CC1的中点,P为AB中点,∴QE
| ∥ |
. |
∴四边形PBEQ是平行四边形,∴BE∥PQ,
过B作BF∥AD,交PC于F,
∵BE∥PQ,BF∥AD,BE∩BF=B,PQ∩PD=P,
BE、BF⊂平面BEF,PQ、PD⊂平面PDQ,
∴平面BEF∥平面PDQ,
∵EF⊂平面BEF,∴EF∥面DPQ.
看了 在四棱柱ABCD-A1B1C...的网友还看了以下:
急如图ABCD是空间四边形它的四条边和两条对角线都相等,E,F分别是AD,BC的中点,求异面直线AF 2020-03-31 …
正方体abcd-a1b1c1d1中mn分别是b1c1,c1d1的中点 求证 m,n,高二数学题 2020-05-13 …
在平行四边形ABCD中,E,F分别是AB,CD上的点,AE=CF,M,N分别是DE,BF的中点求证 2020-05-16 …
如图,在平行四边形ABCD中,BC=2AB=4,点E,F分别是BC,AD的中点 ①求证:ABE全等 2020-05-16 …
如图,ABCD为平行四边形,E、F分别为AB、CD的中点,①求证:AECF也是平行四边形;②连接B 2020-05-16 …
已知在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点,求证:MN与 2020-05-22 …
四边形ABCD是正方形,E是BC的中点,角AEF=90°,AE=EF,G是BC延长线上一点(1)求 2020-05-23 …
在正四面体ABCD中,M,N分别为BC,AD的中点,求异面直线MN与BD所成的角在正四面体(四个面 2020-06-04 …
四边形ABCD中,AB⊥CD,AD‖BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上 2020-06-27 …
冯.奥伯定理求这两条线段相等且垂直任意一个四边形,以每个边为边长,画四个正方形,然后,取这四个正方 2020-07-02 …