早教吧作业答案频道 -->数学-->
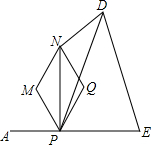
如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是.
题目详情
如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是___.

▼优质解答
答案和解析
作DH⊥PN于H,DF⊥PE于F,连结MQ交PN于O点,如图,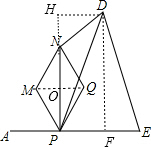 设PA=x,则PM=x,PE=10-x,
设PA=x,则PM=x,PE=10-x,
∵四边形PMNQ为菱形,
∴OP=ON,PN⊥MQ,∠MPO=
∠MPQ=30°,
在Rt△OPM中,∵cos∠MPO=
,
∴PO=x•cos30°=
x,
∴PN=2PO=
x,
∵PN⊥AE,DF⊥PE,DH⊥HP,
∴四边形PFDH为矩形,
∴DH=PF,
∵DP=DE,DF⊥PE,
∴PF=EF=
PE=
(10-x),
∴S△PND=
•PN•DH=
•
x•
(10-x)
=-
(x-5)2+
,
当x=5时,S△PND的值最大,最大值为
.
故答案为
.
 设PA=x,则PM=x,PE=10-x,
设PA=x,则PM=x,PE=10-x,∵四边形PMNQ为菱形,
∴OP=ON,PN⊥MQ,∠MPO=
| 1 |
| 2 |
在Rt△OPM中,∵cos∠MPO=
| OP |
| PM |
∴PO=x•cos30°=
| ||
| 2 |
∴PN=2PO=
| 3 |
∵PN⊥AE,DF⊥PE,DH⊥HP,
∴四边形PFDH为矩形,
∴DH=PF,
∵DP=DE,DF⊥PE,
∴PF=EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PND=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
=-
| ||
| 4 |
25
| ||
| 4 |
当x=5时,S△PND的值最大,最大值为
25
| ||
| 4 |
故答案为
25
| ||
| 4 |
看了 如图,已知线段AE=10,点...的网友还看了以下:
在三角形ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果在AB上找一点E,使三角形AD 2020-05-15 …
如图,D,E是D,A,E三点所在直线m上的两个动点(D,A,E三点互不相重合),且三角形ABF和三 2020-06-13 …
如图,三角形abc中,ad垂直bc于d,e、f分别是ab、ac的中点.当三角形abc满足什么条件, 2020-07-06 …
JAVA创建一个名为设计一个能细分为矩形三角形正方形的“图形”类。1.设计一个能细分为矩形、三角形 2020-07-17 …
如图,bd是三角形abc的角平分线,de垂直ab,垂足为e.三角形abc的面积为70,ab=16, 2020-07-30 …
(2014•潍坊二模)如图所示,在坐标系xoy的第二象限内有沿y轴负方向的匀强电场,电场强度大小为 2020-07-31 …
如图所示,在平面直角坐标系的第一象限虚线左侧有方向沿y轴负方向的有界匀强电场,电场强度大小为E,第 2020-07-31 …
1.正方形ABCD中,AB=12,对角线AC,BD相交于O,则三角形ABO的周长是?2.E为正方形 2020-08-01 …
已知:如图,在三角形ABC中,角ACB=90度,以AB为边在三角形ABC外作三角形ABD,角ADB= 2020-11-03 …
(1)如图,圆O切三角形ABC的BC边于D点,切AB、AC的延长线于E、F,三角形ABC的周长为18 2020-12-25 …