早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,AC=6cm,AB=10cm,点D在边AC上,且点D到边AB和边BC的距离相等.(1)作图:在AC上求作点D;(保留作图痕迹,不写作法)(2)求CD的长.
题目详情
如图,在△ABC中,∠C=90°,AC=6cm,AB=10cm,点D在边AC上,且点D到边AB和边BC的距离相等.
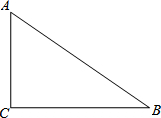
(1)作图:在AC上求作点D;(保留作图痕迹,不写作法)
(2)求CD的长.

(1)作图:在AC上求作点D;(保留作图痕迹,不写作法)
(2)求CD的长.
▼优质解答
答案和解析
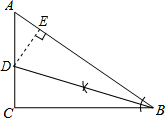 (1)如图所示:
(1)如图所示:
(2)过点D作DE⊥AB,垂足为点E,
∵点D到边AB和边BC的距离相等,
∴BD平分∠ABC.(到角的两边距离相等的点在这个角的平分线上)
∵∠C=90°,DE⊥AB,
∴DC=DE.(角平分线上的点到角的两边的距离相等)
在Rt△CBD和Rt△EBD中,
∴Rt△CBD≌Rt△EBD(HL),
∴BC=BE.
∵在△ABC中,∠C=90°,
∴AB2=BC2+AC2.(勾股定理)
∵AC=6cm,AB=10cm,
∴BC=8cm.
∴AE=10-8=2cm.
设DC=DE=x,
∵AC=6cm,
∴AD=6-x.
∵在△ADE中,∠AED=90°,
∴AD2=AE2+DE2.(勾股定理)
∴(6-x)2=22+x2.
解得:x=
.
即CD的长是
.
 (1)如图所示:
(1)如图所示:(2)过点D作DE⊥AB,垂足为点E,
∵点D到边AB和边BC的距离相等,
∴BD平分∠ABC.(到角的两边距离相等的点在这个角的平分线上)
∵∠C=90°,DE⊥AB,
∴DC=DE.(角平分线上的点到角的两边的距离相等)
在Rt△CBD和Rt△EBD中,
|
∴Rt△CBD≌Rt△EBD(HL),
∴BC=BE.
∵在△ABC中,∠C=90°,
∴AB2=BC2+AC2.(勾股定理)
∵AC=6cm,AB=10cm,
∴BC=8cm.
∴AE=10-8=2cm.
设DC=DE=x,
∵AC=6cm,
∴AD=6-x.
∵在△ADE中,∠AED=90°,
∴AD2=AE2+DE2.(勾股定理)
∴(6-x)2=22+x2.
解得:x=
| 8 |
| 3 |
即CD的长是
| 8 |
| 3 |
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
如图所示,一个带正电的导体A和一个带负电的导体B用带有绝缘柄的金属杆连接时()A.A球上的部分质子 2020-06-18 …
下列叙述正确的是()A.a表示风力侵蚀作用B.b表示风力沉积作用C.c表示流水溶蚀作用D.d表示流 2020-06-19 …
(2006•衡阳)在实验操作考查中,如右图所示是小明同学在用温度计测水的温度时的操作图.A.是操作 2020-06-27 …
已知一次函数y=2x+b.(1)如果它的图象与一次函数y=-2x+1和y=x+4的图象的交于同一点 2020-07-25 …
下列有关生物技术实践的说法正确的是()A.工业生产中只能从植物中提取天然β-胡萝卜素B.电泳法分离各 2020-10-29 …
下列关于传统发酵技术的叙述错误的是()A.家庭制作果酒、果醋、泡菜、腐乳可以不用专门接种B.制作果酒 2020-11-06 …
关于某家庭电路,下列说法正确的是()A.不能用铜丝代替保险丝B.所有家用电器的外壳都要接地C.电灯的 2020-11-14 …
如图所示,在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3kg的金属块B.A的 2020-11-17 …
Excel工作表的数据变化时,由这些数据生成的相应图表将。A.随之改变B.自然消失C.不出现变化D. 2020-11-29 …
下图表示的是四种地貌景观。读图,回答:小题1:表示花岗岩地貌景观的是A.a图B.b图C.c图D.d图 2021-01-15 …