早教吧作业答案频道 -->数学-->
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;(Ⅱ)求三棱锥P-ABC体积的最大值;(Ⅲ)若BC=2,点E在线
题目详情
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
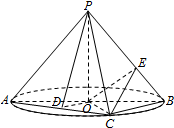
(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;
(Ⅱ)求三棱锥P-ABC体积的最大值;
(Ⅲ)若BC=
,点E在线段PB上,求CE+OE的最小值.

(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;
(Ⅱ)求三棱锥P-ABC体积的最大值;
(Ⅲ)若BC=
| 2 |
▼优质解答
答案和解析
(Ⅰ)在△AOC中,因为OA=OC,D为AC的中点,
所以AC⊥DO,
又PO垂直于圆O所在的平面,
所以PO⊥AC,
因为DO∩PO=O,
所以AC⊥平面PDO.
(Ⅱ)因为点C在圆O上,
所以当CO⊥AB时,C到AB的距离最大,且最大值为1,
又AB=2,所以△ABC面积的最大值为
×2×1=1,
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为:
×1×1=
.
(Ⅲ)在△POB中,PO=OB=1,∠POB=90°,
所以PB=
=
,
同理PC=
,所以PB=PC=BC,
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示,
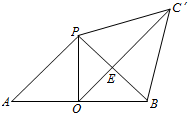 当O,E,C′共线时,CE+OE取得最小值,
当O,E,C′共线时,CE+OE取得最小值,
又因为OP=OB,C′P=C′B,
所以OC′垂直平分PB,即E为PB中点.
从而OC′=OE+EC′=
+
=
.
亦即CE+OE的最小值为:
.
所以AC⊥DO,
又PO垂直于圆O所在的平面,
所以PO⊥AC,
因为DO∩PO=O,
所以AC⊥平面PDO.
(Ⅱ)因为点C在圆O上,

所以当CO⊥AB时,C到AB的距离最大,且最大值为1,
又AB=2,所以△ABC面积的最大值为
| 1 |
| 2 |
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为:
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅲ)在△POB中,PO=OB=1,∠POB=90°,
所以PB=
| 12+12 |
| 2 |
同理PC=
| 2 |
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示,
 当O,E,C′共线时,CE+OE取得最小值,
当O,E,C′共线时,CE+OE取得最小值,又因为OP=OB,C′P=C′B,
所以OC′垂直平分PB,即E为PB中点.
从而OC′=OE+EC′=
| ||
| 2 |
| ||
| 2 |
| ||||
| 2 |
亦即CE+OE的最小值为:
| ||||
| 2 |
看了 如图,AB是圆O的直径,点C...的网友还看了以下:
已知三角形ABC在平面外,它的三边所在直线分别交平面于平面P.Q.R三点求证 pQR三点共线 2020-05-15 …
当拍摄的画面为()时适合于阴影曝光模式。A.主体位于大面积明亮背景前B.逆光拍摄C.以明亮物体为视 2020-05-31 …
( )砖大面有孔,孔多而小,孔洞垂直于大面,孔洞率在l5%以上。 A.烧结普通砖B.烧结多孔砖C. 2020-06-07 …
我国耕地当前面临的问题主要有()A.由于大面积垦荒,耕地不断扩大B.由于大规模植树造林,使耕地迅速 2020-06-27 …
如图所示,两个薄透镜L1和L2共轴放置,已知L1的焦距f1=f,L2的焦距f2=-f,两透镜间的距 2020-07-05 …
如图所示,两个薄透镜L1和L2共轴放置.已知L1的焦距f1=f,L2的焦距f2=-f,两透镜间的距 2020-07-05 …
两个薄透镜L1和L2共轴放置,如图所示.已知L1的焦距f1=f,L2的焦距f2=-f,两透镜间距离 2020-07-22 …
如图所示,重G的风筝用绳子固定于地面P点,风的压力垂直作用于风筝表面AB,并支持着风筝使它平衡.若 2020-07-31 …
客厅是正方形面积是22.4平方米,小明家决定在客厅中铺设地砖,到了大千家居发现又一款正方形地砖非常适 2020-11-13 …
恐龙是不是死于大面积森林火灾造成的大气氧浓度急剧下降地壳运动导致火山频繁,大量的原始森林燃烧造成大气 2020-12-19 …