对于数列{an}，若∀m，n∈N*（m≠n），都有an-amn-m≥t(t为常数)成立，则称数列{an}具有性质P（t）．若数列{an}的通项公式为an=n2-an，且具有性质P（10），

Question

对于数列{a_n}，若∀m，n∈N^*（m≠n），都有 (an-am)/(n-m)≥t(t为常数)成立，则称数列{a_n}具有性质P（t）．若数列{a_n}的通项公式为an=n2- (a)/(n)，且具有性质P（10），则实数a的取值范围是___．

Answer 1

∵数列通项公式an=n2-(a)/(n)且数列具有性质P（10），
∴(an-am)/(n-m)=((n2-(a)/(n))-(m2-(a)/(m)))/(n-m)≥10，
∴((n2-(a)/(n))-(m2-(a)/(m)))/(n-m)-10=((n2-10n-(a)/(n))-(m2-10m-(a)/(m)))/(n-m)≥0恒成立，
∴数列{n2-10n-(a)/(n)}为单调递增数列，
∴(n+1)2-(n+1)-(a)/(n+1)-(n2-10n-(a)/(n))≥0恒成立，
即a≥-n（n+1）（2n-9），
由数轴标根法作图如下，

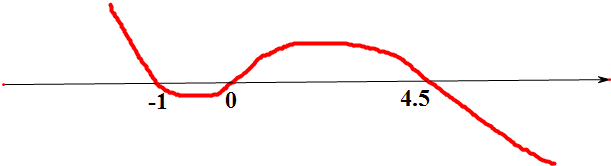
故最大值在n=1，2，3或4上取得，
当n=1时，-n（n+1）（2n-9）=14，
当n=2时，-n（n+1）（2n-9）=30，
当n=3时，-n（n+1）（2n-9）=36，
当n=4时，-n（n+1）（2n-9）=20，
故a≥36．
故答案为：[36，+∞）．