早教吧作业答案频道 -->数学-->
已知,如图(1),PB为O的割线,直线PC与O有公共点C,且PC2=PA×PB,(1)求证:①∠PCA=∠PBC;②直线PC是O的切线;(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求O的半径.
题目详情
已知,如图(1),PB为 O的割线,直线PC与 O有公共点C,且PC2=PA×PB,
(1)求证:①∠PCA=∠PBC;②直线PC是 O的切线;
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求 O的半径.
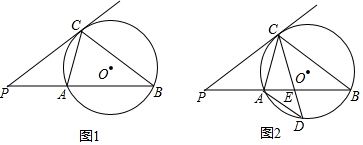
(1)求证:①∠PCA=∠PBC;②直线PC是 O的切线;
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求 O的半径.

▼优质解答
答案和解析
(1)证明:∵PC2=PA×PB,
∴
=
,
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
作直径CF,连接AF,则∠CAF=90°,
∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,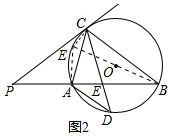
∴直线PC是 O的切线;
(2) 作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
∵CD⊥AB,
∴AE∥CD,
∴
=
,
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2
,
∴ O的半径为
.
∴
| PA |
| PC |
| PC |
| PB |
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
作直径CF,连接AF,则∠CAF=90°,
∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,

∴直线PC是 O的切线;
(2) 作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
∵CD⊥AB,
∴AE∥CD,
∴
 |
| AD |
 |
| CE |
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2
| 10 |
∴ O的半径为
| 10 |
看了 已知,如图(1),PB为O的...的网友还看了以下:
如图,光线沿AB的方向入射,经过B点、C点两处的光景反射后成光线CD.若A、B、C三点的坐标分别为 2020-04-27 …
一质点从A开始做初速度为零的匀加速直线运动中,先后经过B点和C点.已知它的加速度为10m/s2,经 2020-05-14 …
如图,梯形ABCD中,AD‖BC,∠C=45°,AD=5cm,BC=12cm,CD=4根号2cm, 2020-05-16 …
1.某同学蹦极,橡皮绳未拉伸时长45米,绳子绷直时,人的速度是多少2.一个物体从高处A点自由下落, 2020-05-21 …
如图,B,C为定长线段AD上的两个动点(AD长度保持一定,B点在C点的左侧).1,当B,C运动到某 2020-06-05 …
(2009•永州)如图,在平面直角坐标系内,O为原点,点A的坐标为(-3,0),经过A、O两点作半 2020-06-14 …
三角形如何求斜边如:已知ABC三点,A点到B点距离是60,B点到C点距离是50,且B是个直角,求A 2020-06-18 …
一个质点沿直线做加速运动,到A点时速度为3m/s,到B点时速度变为12m/s历时6s;到B点后又做 2020-06-27 …
求某点的加速度时,用v=(s1+s2)/2t,例如BCD三点,求C点的加速度是用B-C的距离+C- 2020-06-29 …
如图,在平面直角坐标系内,O为原点,点A的坐标为(﹣3,0),经过A、O两点作半径为的⊙C,交y轴 2020-07-31 …