早教吧作业答案频道 -->数学-->
如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.(1)求出y与x的函数关系式;(2)为了响应国家号召,
题目详情
如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.
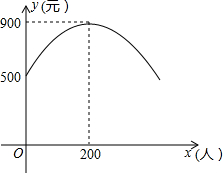
(1)求出y与x的函数关系式;
(2)为了响应国家号召,增加更多的就业机会,又要保证企业的年利润为800万元,那么企业应新招员工多少人?
(3)该企业原有员工400人,那么应招新员工多少人(x>0)时才能使人均创造的年利润与原来的相同,此时的总利润是多少万元?

(1)求出y与x的函数关系式;
(2)为了响应国家号召,增加更多的就业机会,又要保证企业的年利润为800万元,那么企业应新招员工多少人?
(3)该企业原有员工400人,那么应招新员工多少人(x>0)时才能使人均创造的年利润与原来的相同,此时的总利润是多少万元?
▼优质解答
答案和解析
(1)设y与x的函数关系式为y=a(x-200)2+900,
将(0,500)代入,得:a(0-200)2+900=500,
解得:a=-
,
∴y=-
(x-200)2+900;
(2)由题意,得:-
(x-200)2+900=800,
解得:x1=100,x2=300,
∴为增加更多的就业机会,该企业应招新员工300人;
(3)由题意,得:
=
,
整理,得:x2-275x=0,
解得:x1=0(舍),x2=275,
经检验:x=275是原分式方程的解,
当x=275时,y=-
(x-200)2+900=843.75(万元).
答:应招新员工275人时才能使人均创造的年利润与原来的相同,此时的总利润是843.75万元.
将(0,500)代入,得:a(0-200)2+900=500,
解得:a=-
| 1 |
| 100 |
∴y=-
| 1 |
| 100 |
(2)由题意,得:-
| 1 |
| 100 |
解得:x1=100,x2=300,
∴为增加更多的就业机会,该企业应招新员工300人;
(3)由题意,得:
-
| ||
| x+400 |
| 500 |
| 400 |
整理,得:x2-275x=0,
解得:x1=0(舍),x2=275,
经检验:x=275是原分式方程的解,
当x=275时,y=-
| 1 |
| 100 |
答:应招新员工275人时才能使人均创造的年利润与原来的相同,此时的总利润是843.75万元.
看了 如图,抛物线表示的是某企业年...的网友还看了以下:
求已知点关于直线的对称点坐标点A(1,0)关于直线x-y+1=0的对称点,数学老师说把X=1代入直 2020-05-02 …
学校食堂原来每月用煤1.5吨,改进炉灶后,现在每月用煤量只有原来的5分之4.现在每月用煤多少吨?联 2020-06-04 …
统计学计算题(高分)急,(共2道)请哥哥姐姐帮忙!35.某企业产量1992年比1991年高2%,1 2020-07-08 …
英语翻译据统计,俄罗斯国产车的销售量从2004年的88.2万辆减少到2005年的84.1万辆和20 2020-07-12 …
材料一:国家统计局局长王保安称,近几年我国居民消费结构升级改善,恩格尔系数从2013年的31.2% 2020-07-23 …
二、判断题(每题1分,1、今年油菜产量比去年增产,就是().A、今年油菜产量是去年的102%B、去 2020-08-01 …
y=x^2-2x在[0,3]的值域为A,y^2=-x^2+4x+3在[0,m]的值域为B,若A是B 2020-08-01 …
什么是正比例函数?怎么算的?已知y-2与x-1成正比例,当x=2时,y=4,求y与x之间的函数关系 2020-08-03 …
上海城市居民家庭服务性消费保持较快增长态势。抽样调查显示,2010年本市城市居民家庭人均服务性消费支 2020-11-02 …
《江苏省青少年互联网使用状况调查报告(2015年度)》显示,2015年江苏青少年初次接触互联网的平均 2020-11-10 …