早教吧作业答案频道 -->数学-->
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.(1)求证:△APE是等腰直角三角形;(2)若⊙O的直径为2,求PC2+PB2的值.
题目详情
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
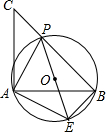
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.

(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
▼优质解答
答案和解析
(1)证明: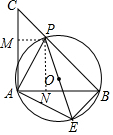 ∵AB=AC,∠BAC=90°,
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=
PM,PB=
PN,
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
 ∵AB=AC,∠BAC=90°,
∵AB=AC,∠BAC=90°,∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=
| 2 |
| 2 |
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
看了 如图,已知等腰直角三角形AB...的网友还看了以下:
如图,B点不动,A点可以在Y轴上任意移动但不能和o点重合,直线AC是直线AB所做的垂线,点D是直线A 2020-03-30 …
已知集合一={k|-o<k<7},集合B=(-∞,-o7)∪(o,+∞),集合C={k|jkj+m 2020-05-14 …
如图,将一副直角三角形叠在一起,使直角顶点重合于点O,则∠AOB=155°,则∠DOC=(),∠C 2020-06-05 …
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装 2020-06-25 …
(12分)如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、 2020-06-29 …
如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且 2020-07-21 …
已知点P的坐标是(-3,4)O是坐标原点,直线L垂直OP,O是垂足,求直线L表示的函数 2020-07-21 …
一道初中几何综合体已知AD是圆O的直径,AB,AC是弦且AB=AC1.求证:直径AD平分角BAC2 2020-07-31 …
如图,已知直线y1=2x-3与y2=-x+3,在平面直角坐标系中相交于点P.(1)求点P的坐标;(2 2020-11-01 …
已知BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD对角线AC,BD交于E.(1)求已知 2020-11-03 …