早教吧作业答案频道 -->数学-->
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC
题目详情
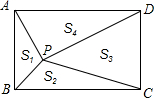
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB~△PDA,则PA=2.4
其中正确的是___(把所有正确的结论的序号都填在横线上)
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB~△PDA,则PA=2.4
其中正确的是___(把所有正确的结论的序号都填在横线上)

▼优质解答
答案和解析
①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①②③④.
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①②③④.
看了 如图,点P是矩形ABCD内一...的网友还看了以下:
立体几何异面直线 相关证明题已知P为△ABC所在平面外一点,PC⊥AB,PC=AB=2,E、F分别 2020-04-05 …
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是P 2020-05-16 …
平面PAD垂直于平面ABCD,三角形PAD是正三角形.ABCD是矩形,M是AB的中点,PC与平面A 2020-05-24 …
如图,在△ABC中,∠C是直角,平面ABC外有一点P,PC=24,点P到直线AC、BC的距离PD和 2020-06-10 …
说明理由1.设N=∫(上面是a,下面是-a)x^2sin^3xdx,P=∫(上面是a,下面是-a) 2020-06-15 …
如图所示,在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、P 2020-07-19 …
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA 2020-07-31 …
立体几何问题在三棱锥P-ABC中,PC⊥AB,二面角P-AB-C为60°,PC与底面成30°角,P 2020-08-02 …
数学立体几何已知∠ACB=90°平面ABC外有一点P,PC=4,P到角的两边AC,BC的距离都等于2 2020-11-02 …
一道高三复习数学题,题型是空间中的角和距离(理科)下午考试,很急,拜托了!PA、PB、PC是从点P引 2020-11-18 …