早教吧作业答案频道 -->数学-->
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,则∠BOC与∠A有
题目详情
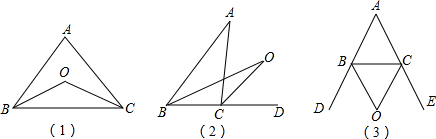
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:___.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:___.
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:___.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:___.

▼优质解答
答案和解析
如图,
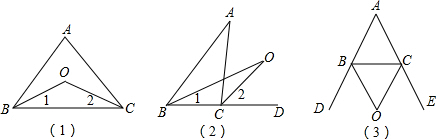
通过分析发现探究2结论:∠BOC=90°+
∠A,
理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,
∴∠1=
∠ABC,∠2=
∠ACB,
∴∠1+∠2=
(∠ABC+∠ACB),
又∵∠ABC+∠ACB=180°-∠A,
∴∠1+∠2=
(180°-∠A)=90°-
∠A,
∴∠BOC=180°-(∠1+∠2),
=180°-(90°-
∠A),
=90°+
∠A;
探究2结论:∠BOC=
∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=
∠ABC,∠2=
∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=
(∠A+∠ABC)=
∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2-∠1=
∠A+∠1-∠1=
∠A;
探究3结论:∠BOC=90°-
∠A.
理由:∵∠OBC=
(∠A+∠ACB),∠OCB=
(∠A+∠ABC),
∴∠BOC=180°-∠0BC-∠OCB,
=180°-
(∠A+∠ACB)-
(∠A+∠ABC),
=180°-
∠A-
(∠A+∠ABC+∠ACB),
∴∠BOC=90°-
∠A.

通过分析发现探究2结论:∠BOC=90°+
| 1 |
| 2 |
理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
又∵∠ABC+∠ACB=180°-∠A,
∴∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠1+∠2),
=180°-(90°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
探究2结论:∠BOC=
| 1 |
| 2 |
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠2是△BOC的一外角,
∴∠BOC=∠2-∠1=
| 1 |
| 2 |
| 1 |
| 2 |
探究3结论:∠BOC=90°-
| 1 |
| 2 |
理由:∵∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠0BC-∠OCB,
=180°-
| 1 |
| 2 |
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=90°-
| 1 |
| 2 |
看了 探究1:如图1,在△ABC中...的网友还看了以下:
如图(a)所示,A、B为两块平行金属板,极板间电压为UAB=1125V,板中央有小孔O和O′.现有 2020-04-06 …
两只小环O和O′分别套在静止不动的竖直杆AB和A′B′上.一根不可伸长的绳子,一端系在A′点上,绳 2020-05-13 …
C3O2的等电子体B2O3B2O3的结构式为O=B-O-B=O对吧,那为什么C3O2的却是O=C= 2020-05-14 …
x^+ax+b=o和x^+cx+15=0的又A∪B={3,5},A∩B={3},求a,b,c的值设 2020-05-16 …
人的血型,常可分为A型、B型、AB型和O型.IAIA和IAi表现为A型;IBIB和IBi表现为B型; 2020-11-03 …
如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O于点C,过点B作两圆的割线分别交⊙ 2020-12-05 …
某人遇车祸急需输血,其血型为B型,血库中B型和O型的血都很充足,应该如何输血()A.只输O型B.先输 2020-12-24 …
用A型标准血清来检验下列几种血型,其中都不发生凝集反应的是()A.B型和O型B.O型和AB型C.A型 2020-12-24 …
关于一道题对功率的提问小环O和O′分别套在不动的竖直杆AB和A′B′上,一根不可伸长的绳子穿过环O′ 2021-01-10 …
如图所示皮带传动装置,皮带轮O和O′上的三点A、B、C,OA=O′C=r,O′B=2r.则皮带轮转动 2021-02-09 …