早教吧作业答案频道 -->数学-->
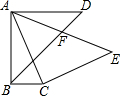
如图,在△ABC中,∠ABC=90°,将AB边绕点A逆时针旋转90°得到线段AD,将AC边绕点C顺时针旋转90°后得到线段CE,AE与BD交于点F,若DF=2,EF=2
题目详情
如图,在△ABC中,∠ABC=90°,将AB边绕点A逆时针旋转90°得到线段AD,将AC边绕点C顺时针旋转90°后得到线段CE,AE与BD交于点F,若DF=
,EF=2
,则BC边的长为___.
| | 2 |
| | 2 |

▼优质解答
答案和解析
如下图所示:
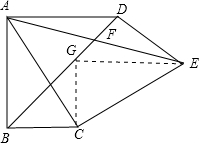
过点C作CG⊥BC,交BD于点G,连接EG,
易证CG=BC,∠BCA=∠GCE,AC=CE,
∴△ABC≌△EGC,
∴GE=AB=AD,∠CEG=∠CAB,
∵∠DAE=90°-45°-∠BAC=45°-∠BAC,而∠AEG=45°-∠CEG,
∴∠DAE=∠AEG
又∵∠AFD=∠EFG(对顶角相等),GE=AD,
∴△AFD≌△EFG,
∴AF=EF,DF=GF,
∴AE=2EF=4
,DG=2
,
∴AC=CE=4
设BC=CG=a,则BG=
a
∴BD=
a+2
,AD=AB=a+2,
在RT△ABC中,(a+2)2+a2=42,
解得a=-
-1(舍去)或a=
-1,
即:BC边的长为
-1

过点C作CG⊥BC,交BD于点G,连接EG,
易证CG=BC,∠BCA=∠GCE,AC=CE,
∴△ABC≌△EGC,
∴GE=AB=AD,∠CEG=∠CAB,
∵∠DAE=90°-45°-∠BAC=45°-∠BAC,而∠AEG=45°-∠CEG,
∴∠DAE=∠AEG
又∵∠AFD=∠EFG(对顶角相等),GE=AD,
∴△AFD≌△EFG,
∴AF=EF,DF=GF,
∴AE=2EF=4
| 2 |
| 2 |
∴AC=CE=4
设BC=CG=a,则BG=
| 2 |
∴BD=
| 2 |
| 2 |
在RT△ABC中,(a+2)2+a2=42,
解得a=-
| 7 |
| 7 |
即:BC边的长为
| 7 |
看了 如图,在△ABC中,∠ABC...的网友还看了以下:
平面上有个9点,其中4个点在同一直线上,此外三点不共线.请问:以一点为端点作为另一点的射线.这样的 2020-05-13 …
设有长度为1,2,…,9的线路各一条,现在要从这9条线段中选取若干条组成一个正方形,共有多少种不同 2020-06-18 …
如图所示线圈面积为0.05m2,共100匝,线圈总电阻为r=1Ω,外电阻R=9Ω,线圈处于B=2π 2020-07-25 …
空间有9点,其中任意4点不共面,在这9个点间连接若干条线段,事图中不存在四面体,则图中三角形最多有为 2020-10-30 …
空间有9点,其中任意4点不共面,在这9个点间连接若干条线段,事图中不存在四面体,则图中三角形最多有为 2020-10-30 …
图9-3-3中的两个线圈,套在一根光滑的玻璃管上。导线柔软,可自由滑动。开关S闭合后,则()图9-3 2020-11-08 …
若直线上有5个点,我们进行第一次操作:在每相邻两点间插入1个点,则直线上有9个点;第二次操作:在9个 2020-11-11 …
这个对角线数独解题规则:从1至9中选数填入空格,使每个数字在每个数独的每一行、每一列、每一个标有粗线 2020-11-18 …
对角线数独游戏2*1*5*6*7*********6**7*1**3**6*4*3**7**2*9* 2020-11-18 …
(1)在一个边长为1的正方形里放3个点,以这3个点为顶点连出的三角形面积最大是多少?(2)在一个边长 2020-12-06 …