如图，平行四边形ABCD中，AB>AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM，若平行四边形ABCD的周长为42，FM=3，EF=4，则AB的长为（

Question

如图，平行四边形ABCD中，AB>AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM，若平行四边形ABCD的周长为42，FM=3，EF=4，则AB的长为（　　）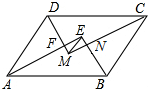

A. 12

B. 13

C. 14

D. 15

Answer 1

∵AE为∠DAB的平分线，
∴∠DAE=∠EAB=(1)/(2)∠DAB，
同理：∠ABE=∠CBE=(1)/(2)∠ABC，
∠BCM=∠DCM=(1)/(2)∠BCD，
∠CDM=∠ADM=(1)/(2)∠ADC．
∵四边形ABCD是平行四边形，
∴∠DAB=∠BCD，∠ABC=∠ADC，AD=BC．
∴∠DAF=∠BCN，∠ADF=∠CBN．
在△ADF和△CBN中，
∵

∠DAF=∠BCN

AD=CB

∠ADF=∠CBN

，
∴△ADF≌△CBN（ASA）．
∴DF=BN．
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAB+∠ABC=180°．
∴∠EAB+∠EBA=90°．
∴∠AEB=90°．
同理可得：∠AFD=∠DMC=90°．
∴∠EFM=90°．
∵FM=3，EF=4，
∴ME=√(32+42)=5（cm）．
∵∠EFM=∠FMN=∠FEN=90°．
∴四边形EFMN是矩形．
∴EN=FM=3．
∵∠DAF=∠EAB，∠AFD=∠AEB，
∴△AFD∽△AEB．
∴(DF)/(BE)=(AF)/(AE)，
∴(DF)/(3+DF)=(AF)/(4+AF)，
∴4DF=3AF．
设DF=3k，则AF=4k．
∵∠AFD=90°，
∴AD=5k．
∵∠AEB=90°，AE=4（k+1），BE=3（k+1），
∴AB=5（k+1）．
∵2（AB+AD）=42，
∴AB+AD=21．
∴5（k+1）+5k=21．
∴k=1.6．
∴AB=13（cm）．
故选B．