早教吧作业答案频道 -->数学-->
把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.(1)如图1,求证:BE=AD,AF⊥BE;(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别
题目详情
把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
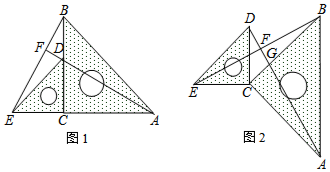
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.

▼优质解答
答案和解析
(1)证明:在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACD中,
∵∠CDA+∠CAD=90°,∠BDF=∠CDA
∴∠BDF+∠DBF=90°,
即:AF⊥BE;
(2)成立,理由如下:
在△BCE和△ACD中,
∵∠BCE=∠ACD=90°,
∴∠DCE+∠DCB=∠ACB+∠BCD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACG中,
∵∠CGA+∠CAG=90°,∠BGF=∠CGA.
∴∠BGF+∠GBF=90°,
即:AF⊥BE.
|
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACD中,
∵∠CDA+∠CAD=90°,∠BDF=∠CDA
∴∠BDF+∠DBF=90°,
即:AF⊥BE;
(2)成立,理由如下:
在△BCE和△ACD中,
∵∠BCE=∠ACD=90°,
∴∠DCE+∠DCB=∠ACB+∠BCD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACG中,
∵∠CGA+∠CAG=90°,∠BGF=∠CGA.
∴∠BGF+∠GBF=90°,
即:AF⊥BE.
看了 把两块含45°角的直角三角板...的网友还看了以下:
如图,在矩形ABCD中,AB=5,AD=8,直角尺的直角顶点E在AD上滑动时如图,在矩形ABCD中 2020-05-17 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
如图,矩形ABCD中,AB=6,AD=8,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′, 2020-06-13 …
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ADC=120°. 将一块足够大的三角 2020-06-27 …
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,将 2020-07-18 …
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得出线段BE 2020-07-19 …
如图,Rt△ABC中,AB=AC=4,D是AC中点延长BA至E使AD=AE,将△ADE绕点A逆时针 2020-07-22 …
△ABC中,AB=AC=10,E是平面内一点,作∠EBC=∠BED=60,D在∠BAC平分线上,B 2020-07-31 …
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,将∠ 2021-02-04 …