早教吧作业答案频道 -->数学-->
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△
题目详情
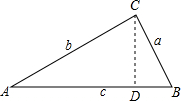
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
∴BD=c-bcosA
在Rt△BDC中,由勾股定理:CD2+BD2=BC2
(c-bcosA)2+(bsinA)2=a2,整理得:a2=b2+c2-2bccosA
同理可得:b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
利用上述结论解答下列问题:
(1)锐角在△ABC中,∠A=45°,b=2
,c=2,求a和∠C的大小
(2)在△ABC中,a=
,b=
,∠B=45°,(c>a>b),求边长c的长度.
∴BD=c-bcosA
在Rt△BDC中,由勾股定理:CD2+BD2=BC2
(c-bcosA)2+(bsinA)2=a2,整理得:a2=b2+c2-2bccosA
同理可得:b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
利用上述结论解答下列问题:

(1)锐角在△ABC中,∠A=45°,b=2
| 2 |
(2)在△ABC中,a=
| 3 |
| 2 |
▼优质解答
答案和解析
(1)在锐角△ABC中,a2=b2+c2-2bccosA
=(2
)2+4-2×2
×2×
=4
解得,a=2,
22+22=(2
)2
∴△ABC为直角三角形,a=c=2,
∴∠C=45°;
(2)∵b2=a2+c2-2accosB,
∴c2-
c+1=0,
解得,c=
,
∵c>a>b,
∴c=
.
=(2
| 2 |
| 2 |
| ||
| 2 |
=4
解得,a=2,
22+22=(2
| 2 |
∴△ABC为直角三角形,a=c=2,
∴∠C=45°;
(2)∵b2=a2+c2-2accosB,
∴c2-
| 6 |
解得,c=
| ||||
| 2 |
∵c>a>b,
∴c=
| ||||
| 2 |
看了 我们知道,直角三角形的边角关...的网友还看了以下:
a,b,c成等差数列,a+1,b+1,c+4成等比数列,求a,b,c我自己做了N久也是两个方程三格 2020-05-16 …
如图,把三角形ABC绕原点O旋转180度后得到三角形A'B'C',则三角形A'B'C'的坐标分别为 2020-05-16 …
在三角形ABC中,已知2sin^2(A)=3sin^2(B)+3sin^2(C),cos(2A)+ 2020-06-03 …
求极限的时候形如(A+B)/C,什么时候能拆成A/C+B/C的形式呢为什么x趋近于0时,{ln(1 2020-06-22 …
离子晶体中层A,B,C的代表意义不妨举一例,下为某题的一部分:某晶体阴离子为立方最密堆积,有A,B 2020-06-23 …
1.(2x-3y-4z)的平方(不知如何解)2.(A-B)^2(A-B)3(A-B)^4(A-B)^ 2020-10-31 …
1÷2/3的写法正确吗就是A÷B/C,A除以一个分数,不知道除号和分数形式能不能一起用,还是要写成A 2020-11-16 …
绝对值化简,我不要解题的方式,要方法,如|a+b-c|只抄a+b-c,我要的不是解题过程,而是方法方 2020-12-12 …
如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0),将矩形OABC绕原点O顺时 2020-12-25 …
已知A(0,-2),B(-2,1),C(3,2)求线段AB,BC,AC.把A、B、C三点的横坐标、纵 2020-12-25 …