（1）如图，在锐角△ABC中，利用三角函数的定义及勾股定理证明你的猜想；（2）已知∠A为锐角（cosA>0）且sinA=35，求cosA．

Question

（1）如图，在锐角△ABC中，利用三角函数的定义及勾股定理证明你的猜想；
（2）已知∠A为锐角（cosA>0）且sinA=(3)/(5)，求cosA．

Answer 1

（1）猜想：BC²=AB²+AC²-2AB•AC•cosA．
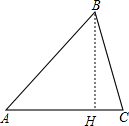
证明如下：作BH⊥AC于H，如图，
在Rt△ABH中，AB²=AH²+BH²，cosA=(AH)/(AB)，即AH=AB•cosA，
在Rt△CBH中，BC²=CH²+BH²，
而CH=AC-AH，
则BC²=（AC-AH）²+BH²=AC²-2AC•AH+AH²+BH²，
所以BC²=AC²-2AC•AB•cosA+AB²，
即BC²=AB²+AC²-2AB•AC•cosA．
（2）∵sin²A+cos²A=1，
∴cosA=√(1-sin2A)=√(1-((3)/(5))2)=(4)/(5)．