早教吧作业答案频道 -->数学-->
如图①,在Rt△ABC中,∠ACB=90°,AC=BC,l是过点C的任意一条直线,过A作AD⊥l于D,过B作BE⊥l于E.(1)求证:△ACD≌△ACD;(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°
题目详情
如图①,在Rt△ABC中,∠ACB=90°,AC=BC,l是过点C的任意一条直线,过A作AD⊥l于D,过B作BE⊥l于E.
(1)求证:△ACD≌△ACD;
(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°,连接AG交l于H.求证:BF=2CH.
(3)在(2)的条件下,若AD=12,BE=15,BC=13,请直接写出点G到直线AC的距离.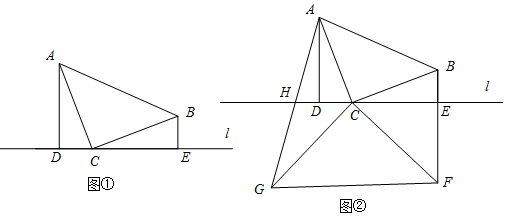
(1)求证:△ACD≌△ACD;
(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°,连接AG交l于H.求证:BF=2CH.
(3)在(2)的条件下,若AD=12,BE=15,BC=13,请直接写出点G到直线AC的距离.

▼优质解答
答案和解析
(1)证明:如图①中,
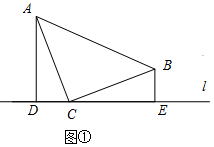
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=∠ACB=90°,
∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS).
(2)如图②中,作AM∥CG交EH于M,连接GM.
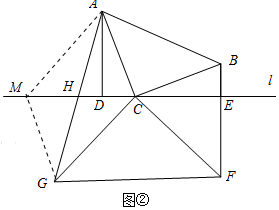
∵∠MAC+∠ACG=180°,∠ACG+∠BCF=180°,
∴∠MAC=∠BCF,
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACM=∠CBF,
在△ACM和△CBF中,
,
∴△MAC≌△CBF,
∴CM=BF,AM=CF=CG,∵AM∥CG,
∴四边形AMGC是平行四边形,
∴MH=HC,
∴BF=CM=2CH.
(3)∵△MAC≌△CBF,
∴CM=BF=15,
∵AC=BC=13,
∴S四边形AMCG=2•S△AMC=AC•h(h是点G到AC的距离),
∴2×
×15×12=13h,
∴h=

∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=∠ACB=90°,
∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS).
(2)如图②中,作AM∥CG交EH于M,连接GM.

∵∠MAC+∠ACG=180°,∠ACG+∠BCF=180°,
∴∠MAC=∠BCF,
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACM=∠CBF,
在△ACM和△CBF中,
|
∴△MAC≌△CBF,
∴CM=BF,AM=CF=CG,∵AM∥CG,
∴四边形AMGC是平行四边形,
∴MH=HC,
∴BF=CM=2CH.
(3)∵△MAC≌△CBF,
∴CM=BF=15,
∵AC=BC=13,
∴S四边形AMCG=2•S△AMC=AC•h(h是点G到AC的距离),
∴2×
| 1 |
| 2 |
∴h=
| 180 |
| 13 |
看了 如图①,在Rt△ABC中,∠...的网友还看了以下:
绳子下悬挂一物体,在力f的作用下,静止.绳子与竖直方向的夹角为10度.当f=g时,f与竖直方向夹角多 2020-03-30 …
一道数学微分方程的题假设:(1)函数y=f(x)(0≤x<+∞)满足条件f(0)=0和0≤f(x) 2020-05-13 …
双曲线的中心为原点O,焦点在x轴上,两条渐进线分别为L1,L2,经过右焦点F且垂直于L1的直线L分 2020-05-13 …
若f(x)=x^2+x,则f(-1)=,f(-x)=,f(x-1)=直角三角形ABC中,斜边AC= 2020-05-14 …
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴的距离的差都是1.(1)求曲 2020-05-15 …
将力F分解为F1和F2,若已知F1的大小和F2与F的夹角α(锐角)之前看到您说当F1<Fsinα时 2020-06-05 …
一道关于函数周期的题若函数f(x)在R上为奇函数,且在(-1,0)上为增函数,且f(x+2)=-f 2020-06-07 …
求详解:函数已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x²,当x≥0时,f(x+ 2020-06-09 …
1双曲线的一个焦点为F过F作垂直于实轴的直线交双曲线于AB两点若以AB为直径的圆恰好过双曲线的一个 2020-07-30 …
等腰直角三角形ABC,斜边BC,点D、E在AC、CA的延长线上,AE=CD,连DB,AM垂直BD于M 2020-12-25 …