早教吧作业答案频道 -->数学-->
如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.(1)试判定四边形AEDF的形状,并证明你的结论.(2)若AE=5,AD=8,求EF的长.(3)△ABC满足什么条件时
题目详情
如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
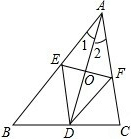
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若AE=5,AD=8,求EF的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?

(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若AE=5,AD=8,求EF的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
▼优质解答
答案和解析
(1)四边形AEDF是菱形,
∵AD平分∠BAC,
∴∠1=∠2,
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
∵在△AEO和△AFO中
∵
,
∴△AEO≌△AFO(ASA),
∴EO=FO,
∵EF垂直平分AD,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形
又EF⊥AD,
∴平行四边形AEDF为菱形;
(2)∵EF垂直平分AD,AD=8,
∴∠AOE=90°,AO=4,
在RT△AOE中,∵AE=5,
∴EO=
=3,
由(1)知,EF=2EO=6;
(3)当△ABC中∠BAC=90°时,四边形AEDF是正方形;
∵∠BAC=90°,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).
∵AD平分∠BAC,
∴∠1=∠2,
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
∵在△AEO和△AFO中
∵
|
∴△AEO≌△AFO(ASA),
∴EO=FO,
∵EF垂直平分AD,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形
又EF⊥AD,
∴平行四边形AEDF为菱形;
(2)∵EF垂直平分AD,AD=8,
∴∠AOE=90°,AO=4,
在RT△AOE中,∵AE=5,
∴EO=
| AE2-AO2 |
由(1)知,EF=2EO=6;
(3)当△ABC中∠BAC=90°时,四边形AEDF是正方形;
∵∠BAC=90°,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).
看了 如图,AD是△ABC的角平分...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
(2013•百色)如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的 2020-05-16 …
已知,如图,在平行四边形ABCD中,DE、BF分别平分∠ADC与∠ABC,交AB于点E、交CD于点 2020-05-16 …
如图所示,在空间四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA上的一点,且EFGH为 2020-05-16 …
如图9,在四边形ABCD中,点E在线段CD上,=如图9,在四边形ABCD中,点E在线段CD上,DC 2020-06-04 …
已知AC、BC分别平分角QAB、角ABN,且角1与角2互余.1.如图一,求证:PQ平行于MN2.过 2020-06-07 …
已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、F是对角线上的两点,且AE⊥ 2020-06-12 …
如图CM、CN分别△ABC的内角、外角平分线,O是AC上的点,直线L经过点O且L‖BC交CM如图C 2020-07-20 …
如图1,在△ABC中,若AD是∠BAC的角平分线,过D点分别作DE⊥AB,DF⊥AC,垂足分别为E 2020-07-22 …
如图所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点.过点E的直线分别交AM、DN 2020-11-28 …