早教吧作业答案频道 -->数学-->
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.(1)求m的值;(2)求这条抛物线的表达式;(3)点P在抛物线上,点Q在x轴上,当∠PQ
题目详情
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.
(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.
▼优质解答
答案和解析
(1)当x=0时,y=-3,
∴D(0,-3).
设抛物线的解析式为y=a(x-m)(x-6m).
把点D和点A的坐标代入得:6am2=-3①,a(7-m)(7-6m)=-3②,
∴a(7-m)(7-6m)=6am2.
∵a≠0,
∴(7-m)(7-6m)=m2.
解得:m=1.
(2)∵6am2=-3,
∴a=-
=-
.
将a=-
,m=1代入得:y=-
x2+
x-3.
∴抛物线的表达式为y=-
x2+
x-3.
(3)如图所示:过点P作PE⊥x轴,垂足为E.
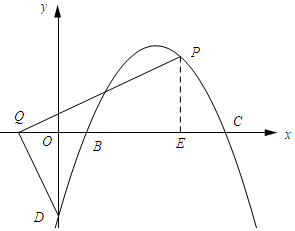
设点Q的坐标为(a,0)则OQ=-a
-∵∠DQP=90°,
∴∠PQO+∠OQD=90°.
又∵∠ODQ+∠DQO=90°,
∴∠PQE=∠ODQ.
又∵∠PEQ=∠DOQ=90°,
∴△ODQ∽△EQP.
∴
=
=
=
,即
=
=
,
∴QE=6,PE=-2a.
∴P的坐标为(a+6,-2a)
将点P的坐标代入抛物线的解析式得:-
(a+6)2+
(a+6)-3=-2a,整理得:a2+a=0,
解得a=-1或a=0.
当a=-1时,Q(-1,0),P(5,2);当a=0时,Q(0,0),P(6,0).
综上所述,Q(-1,0),P(5,2)或者Q(0,0),P(6,0).
∴D(0,-3).
设抛物线的解析式为y=a(x-m)(x-6m).
把点D和点A的坐标代入得:6am2=-3①,a(7-m)(7-6m)=-3②,
∴a(7-m)(7-6m)=6am2.
∵a≠0,
∴(7-m)(7-6m)=m2.
解得:m=1.
(2)∵6am2=-3,
∴a=-
| 3 |
| 6m2 |
| 1 |
| 2 |
将a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴抛物线的表达式为y=-
| 1 |
| 2 |
| 7 |
| 2 |
(3)如图所示:过点P作PE⊥x轴,垂足为E.

设点Q的坐标为(a,0)则OQ=-a
-∵∠DQP=90°,
∴∠PQO+∠OQD=90°.
又∵∠ODQ+∠DQO=90°,
∴∠PQE=∠ODQ.
又∵∠PEQ=∠DOQ=90°,
∴△ODQ∽△EQP.
∴
| QO |
| PE |
| OD |
| QE |
| QD |
| QP |
| 1 |
| 2 |
| -a |
| 3 |
| PE |
| 6 |
| 1 |
| 2 |
∴QE=6,PE=-2a.
∴P的坐标为(a+6,-2a)
将点P的坐标代入抛物线的解析式得:-
| 1 |
| 2 |
| 7 |
| 2 |
解得a=-1或a=0.
当a=-1时,Q(-1,0),P(5,2);当a=0时,Q(0,0),P(6,0).
综上所述,Q(-1,0),P(5,2)或者Q(0,0),P(6,0).
看了 已知:抛物线y=ax2+bx...的网友还看了以下:
2-氯-1,3-丁二烯的逆合成分析为:CH2CCLCH2------>HOCH2CHCLCH2CH 2020-06-11 …
为什么说空间几何中线与线的平行是异面.求数学帝解答,十分感谢.平行:在平面上两条直线、空间的两个平 2020-07-21 …
线与线的夹角为(0°,90°]面与面的夹角为(0°,180°],为什么0°取不到 2020-07-30 …
填空:(1)的名称是(2)的名称是(3)2-丁醇的键线式为(4)CH2=CH-CH=CH2一定条件下 2020-11-07 …
(2014•郴州)读湖南省地图,回答下列问题.(1)湖南省的行政中心是,最重要的河流A是.(2)湖南 2020-11-12 …
读湖南省地图,回答问题.(1)山脉①是,邻省②是.铁路交通枢纽③是,是沪昆线与线的交汇.湖南与广东的 2020-11-12 …
某城市地铁一期工程分高架线和地下线两部分.其中高架线长约6.5千米,地下线的长度比高架线的1.6倍少 2020-11-20 …
南京地铁一期工程分高架线和地下线两部分,其中高架线长约6.5千米,地下线是高架线的1.6倍,第一期工 2020-11-20 …
南京地铁一期工程分高架线和地下线两部分,其中高架线长约6.5千米,地下线是高架线的1.6倍,第一期工 2020-11-20 …
南京地铁一期工程分高架线和地下线两部分,其中地下线是高架线的1.6倍,地下线的长度比高架线长3.9千 2020-11-20 …