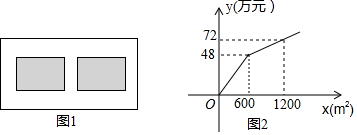
为创建生态文明城市，某小区将一块长60米，宽40米的矩形空地，计划修筑成两块相同的绿色植物园，两块绿色植物园之间及周边留有宽度相同的人行通道（如图1所示），设人行通道宽为a米

Question

为创建生态文明城市，某小区将一块长60米，宽40米的矩形空地，计划修筑成两块相同的绿色植物园，两块绿色植物园之间及周边留有宽度相同的人行通道（如图1所示），设人行通道宽为a米，小区经过与某园林公司协商修建道路费用为10万元，但修建绿色植物园的造价y（万元）与修建面积x（米²）之间的函数关系如图2所示，如果小区决定由该公司修建此工程，并且要求道路的宽度不少于4米但不要超过10米
（1）用含a的式子表示绿色植物园的面积S（米²）；
（2）如果人行通道的面积是864米²，求人行通道宽度；
（3）写出工程总造价W（万元）与人行通道的宽a（米）之间的函数关系，并求当人行通道宽为多少米时，工程总造价最低，最低造价为多少万元？

Answer 1

（1）根据题意得：S=（60-3a）（40-2a）=6a²-240a+2400（4≤a≤10）；

（2）根据绿色植物园的面积S等于矩形面积减去人行道的面积得：6a²-240a+2400=60×40-864，
解得：a₁=4，a₂=36>10（舍去），
∴人行通道宽度为4米；

（3）

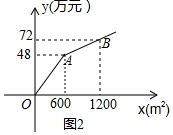
设OA的解析式为y₁=kx，
把x=600、y=48代入，得：600k=48，
∴k=(2)/(25)，
∴y₁=(2)/(25)x（0<x≤600），
设AB的解析式为y₂=kx+b，
把x=600、y=48，x=1200、y=72，代入，
得：

600k+b=48

1200k+b=72

，
解得：

k=(1)/(25)

b=24

，
∴y=(1)/(25)x+24，
∴w₁=y₁+10=(2)/(25)x+10=(2)/(25)（6a²-240a+2400）+10=(12)/(25)（a-20）²+10（4≤a≤10）；
∵0≤6a²-240a+2400≤600，
解得：10≤a≤20，
∴a=10时，w₁=(12)/(25)（10-20）²+10=58；
w₂=y₂+10=(1)/(25)x+24+10=(1)/(25)（6a²-240a+2400）+24+10=(6)/(25)（a-20）²+34，
∵6a²-240a+2400≥600，
∴a≤10或a≥30，
∵当a<20时，w₂随a的增大而减小，且4≤a≤10，
∴当a=10时，w₂取得最小值，w₂=(6)/(25)（10-20）²+34=58，
综上，求当人行通道宽为10米时，工程总造价最低，最低造价为58万元．