早教吧作业答案频道 -->数学-->
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.(1)求证:△BOC≌△CDA;(2)若AB=2,求阴影部分的面积.
题目详情
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
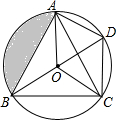
(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.

(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.
▼优质解答
答案和解析
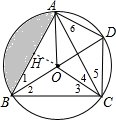 (1)证明:∵O是△ABC的内心,
(1)证明:∵O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
,
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠BOH=
(180°-120°)=30°,
∵OH⊥AB,
∴BH=AH=
AB=1,
OH=
BH=
,
OB=2OH=
,
∴S阴影部分=S扇形AOB-S△AOB
=
-
×2×
=
.
 (1)证明:∵O是△ABC的内心,
(1)证明:∵O是△ABC的内心,∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
|
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠BOH=
| 1 |
| 2 |
∵OH⊥AB,
∴BH=AH=
| 1 |
| 2 |
OH=
| ||
| 3 |
| ||
| 3 |
OB=2OH=
2
| ||
| 3 |
∴S阴影部分=S扇形AOB-S△AOB
=
120•π•(
| ||||
| 360 |
| 1 |
| 2 |
| ||
| 3 |
=
4π-3
| ||
| 9 |
看了 如图,O是△ABC的内心,B...的网友还看了以下:
已知圆心为C的圆经过点A(0,1)和B(-2,3),且圆心直线L:x+2y-3=0上1求圆C标准方 2020-04-27 …
PS测试题,继续回答.27在FlashMX中,要绘制基本的几何形状,可以使用的绘图工具是:A直线B 2020-06-03 …
已知直线L:y=kx+1和椭圆c:x2/4+y2/2=1,相较于A,B两点,已知定点D(0,1)使 2020-07-03 …
已知椭圆C:X2/a2Y2/b2=1(a>b>0)的短轴长2根号3,右焦点F与抛物线y2=4x的焦 2020-07-13 …
如图,在平面直角坐标系xoy中,已知点A为椭圆x29+2y29=1的右顶点,点D(1,0),点P, 2020-07-24 …
给定点A(x,y),圆C:x2+y2=r2及直线l:xx+yy=r2,给出以下三个命题:①当点A在 2020-07-26 …
已知圆O:x2+y2=4和圆C:x2+(y-4)2=1.(Ⅰ)判断圆O和圆C的位置关系;(Ⅱ)过圆 2020-07-26 …
圆O的半径r为13厘米,圆心O到直线l的距离OD为5厘米,点A,B,C在直线上若DA=13,则点A 2020-07-26 …
已知椭圆C:X2/a2+Y2/b2=1(a>b>0)的短轴长2根号3,右焦点F与抛物线y2=4x的 2020-07-31 …
AB是圆O的弦,OD垂直AB于C,DA与圆O相切于A,若AB=8,其弦心距=3.则DA=一楼不对吧 2020-08-01 …