早教吧作业答案频道 -->数学-->
如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.(1)若∠BOE=64°,求∠DOF和∠AOC的度数;(2)试问∠COE与∠BOE之间有怎样的大小关系?为什么?
题目详情
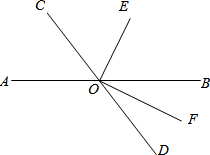 如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.
如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.(1)若∠BOE=64°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?为什么?
▼优质解答
答案和解析
考点:
对顶角、邻补角 角平分线的定义 垂线
专题:
分析:
(1)根据余角的性质,可得∠BOF的度数,根据角平分线的性质,可得∠DOF的度数、∠BOD的度数,根据对顶角相等,可得答案;(2)根据角的和差,可得∠COE的度数,根据角的大小比较,可得答案.
(1)由OE⊥OF,∠BOE=64°,得∠BCF=∠EOF-∠BOE=90°-64°=26°.由OF是∠BOD的平分线,得∠DOF=∠BOF=26°,∠BOD=2∠BOF=52°,由对顶角相等,得∠AOC=∠BOD=52°;(2)∠COE=∠BOE,理由如下:由角的和差,得∠COB+∠BOD=180°,即12∠COB+12∠BOD=12×180°=90°①,∠EOF=∠BOE+∠BOF=90°,∠BOF=12∠BOD,∠BOE+12∠BOD=90°②①-②,得12∠COB-∠BOE=0.即12∠COB=∠BOE.
点评:
本题考查了对顶角、邻补角,利用了角的和差,角平分线的性质,对顶角相等的性质.
考点:
对顶角、邻补角 角平分线的定义 垂线
专题:
分析:
(1)根据余角的性质,可得∠BOF的度数,根据角平分线的性质,可得∠DOF的度数、∠BOD的度数,根据对顶角相等,可得答案;(2)根据角的和差,可得∠COE的度数,根据角的大小比较,可得答案.
(1)由OE⊥OF,∠BOE=64°,得∠BCF=∠EOF-∠BOE=90°-64°=26°.由OF是∠BOD的平分线,得∠DOF=∠BOF=26°,∠BOD=2∠BOF=52°,由对顶角相等,得∠AOC=∠BOD=52°;(2)∠COE=∠BOE,理由如下:由角的和差,得∠COB+∠BOD=180°,即12∠COB+12∠BOD=12×180°=90°①,∠EOF=∠BOE+∠BOF=90°,∠BOF=12∠BOD,∠BOE+12∠BOD=90°②①-②,得12∠COB-∠BOE=0.即12∠COB=∠BOE.
点评:
本题考查了对顶角、邻补角,利用了角的和差,角平分线的性质,对顶角相等的性质.
看了 如图,直线AB与CD相交于O...的网友还看了以下:
AB为圆O的直径点C为圆O上一点AD和过点C的切线互相垂直垂足为点D过点C作CE垂直AB垂足为点E直 2020-03-30 …
如图,AB是圆O的直径,CD切圆O于点C,AD交于圆O点E,当AC满足什么条件时,AD垂直于CD, 2020-05-15 …
如图,▱ABCD中,AB⊥AC,AB=1,BC=5,对角线BD、AC交于点O.将直线AC绕点O顺时 2020-06-12 …
如图,AB是⊙O的直径,DF切⊙O于点D,BF⊥DF于F,过点A作AC∥BF交BD的延长线于点C. 2020-06-15 …
下图,⊙O的半径为2,弧AB等于120°,E是劣弧AB的中点.(1)下图①,试说明:点O、E关于A 2020-06-23 …
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于 2020-06-27 …
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合 2020-07-21 …
(2014•营口模拟)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂 2020-07-22 …
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E 2020-07-31 …
(2008•安顺)已知:如图,正方形ABCD中,对角线AC和BD相交于点O.E、F分别是边AB、BC 2020-11-13 …