早教吧作业答案频道 -->数学-->
如图,AD是△ABC的高,点E,F在边BC上,点H在边AB上,点G在边AC上,AD=80cm,BC=120cm.(1)若四边形EFGH是正方形,求正方形的面积.(2)若四边形EFGH是长方形,长方形的面积为y,设EF=x,则y=
题目详情
如图,AD是△ABC的高,点E,F在边BC上,点H在边AB上,点G在边AC上,AD=80cm,BC=120cm.
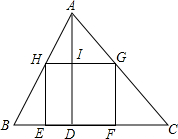
(1)若四边形EFGH是正方形,求正方形的面积.
(2)若四边形EFGH是长方形,长方形的面积为y,设EF=x,则y=___.(含x的代数式),当x=___时,y最大,最大面积是___.
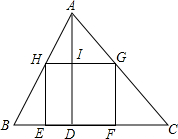
(1)若四边形EFGH是正方形,求正方形的面积.
(2)若四边形EFGH是长方形,长方形的面积为y,设EF=x,则y=___.(含x的代数式),当x=___时,y最大,最大面积是___.
▼优质解答
答案和解析
(1)∵四边形EFGH是正方形,
∴HG∥EF,GH=HE=ID,
∴△AHG∽△ABC,
∴AI:AD=HG:BC,
∵BC=120cm,AD=80cm,
∴
=
,
解得:HG=48cm,
∴正方形EFGH的面积=HG2=482=2304(cm2);
(2)∵四边形EFGH是长方形,
∴HG∥EF,
∴△AEF∽△ABC,
∴AI:AD=HG:BC,
即
=
,
解得:HE=-
x+80,
∴长方形EFGH的面积y=x(-
x+80)=-
x2+80x=-
(x-60)2+240,
∵-
<0,
∴当x=60,即EF=60cm时,长方形EFGH有最大面积,最大面积是240cm2;
故答案为:-
x2+80x,60cm,240cm2.
∴HG∥EF,GH=HE=ID,
∴△AHG∽△ABC,
∴AI:AD=HG:BC,
∵BC=120cm,AD=80cm,
∴
| 80-HG |
| 80 |
| HG |
| 120 |
解得:HG=48cm,
∴正方形EFGH的面积=HG2=482=2304(cm2);
(2)∵四边形EFGH是长方形,
∴HG∥EF,
∴△AEF∽△ABC,
∴AI:AD=HG:BC,
即
| 80-HE |
| 80 |
| x |
| 120 |
解得:HE=-
| 2 |
| 3 |
∴长方形EFGH的面积y=x(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∵-
| 2 |
| 3 |
∴当x=60,即EF=60cm时,长方形EFGH有最大面积,最大面积是240cm2;
故答案为:-
| 2 |
| 3 |
看了 如图,AD是△ABC的高,点...的网友还看了以下:
A平行四边形四条边一定相等B平行四边形对边平行且相等C长方形是特殊平行四边形D平行四边形对角一定相 2020-04-26 …
1.它是一个平行四边形,别且有四个直角()2.它是四条边都相等的平行四边形,并且有四个直角()选择 2020-05-15 …
把一个长18厘米宽12厘米的长方形木框拉成一个平行四方形,使平行四边形的高是长方形的一半;问:(1 2020-05-15 …
空间四边形的四条边长度相等,则顺次连接这个四边形各边中点所得的图形是()A.矩形B.菱形C.正方形 2020-06-06 …
如果在四边形内存在一点,它到四个顶点的距离相等,那么这个四边形一定是()A.平行四边形B.矩形C. 2020-07-30 …
两个完全一样的三角形不可能拼成一个().A长方形B平行四边形C正方形D两个完全一样的三角形不可能拼成 2020-11-03 …
a四方+b四方+c四方+d四方=4abcd,abcd为正数,用abcd围成的图形是什么图形不是正方形 2020-11-07 …
三角形ABC中a,b,c三边满足a四方+b四方+c四方=2c平方(a平方+b平方)求C=? 2020-11-07 …
如果一个平行四边形的一个角变为直角,这个四边形是()A.长方形B.正方形C.长方形或正方形 2020-11-08 …
方程|x-1|+|y-1|=1表示的图形是()A.1个点B.四条直线C.正方形D.四个点PS:为什么 2020-11-27 …