早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,BC=6,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,当点P运动到A时,点P、Q随即停止运动,若点P、Q移动的速度相同,PQ与直线BC相交于点D.
题目详情
如图,在△ABC中,AB=AC,BC=6,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,当点P运动到A时,点P、Q随即停止运动,若点P、Q移动的速度相同,PQ与直线BC相交于点D.
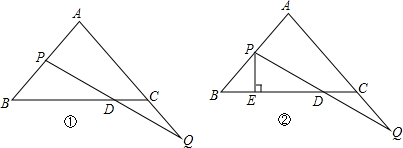
(1)如图①,当点P自点B出发在线段BA上运动是,过点P作AC的平行交BC于点F,连接PC、FQ,判断四边形PFQC的形状,并证明你的结论.
(2)如图②,过点P作PE⊥BC,垂足为E,请说明在点P、Q在移动的过程中,DE长度保持不变.
(1)如图①,当点P自点B出发在线段BA上运动是,过点P作AC的平行交BC于点F,连接PC、FQ,判断四边形PFQC的形状,并证明你的结论.
(2)如图②,过点P作PE⊥BC,垂足为E,请说明在点P、Q在移动的过程中,DE长度保持不变.

▼优质解答
答案和解析
(1)如图①中,四边形PFQC是平行四边形.
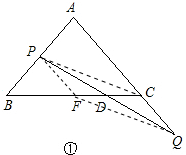
理由:∵AB=AC,
∴∠B=∠ACB,
∵PF∥AQ,
∴∠PFB=∠ACB=∠B,∠DPF=∠DQC,
∴PB=PF=CQ,
在△DPF和△DQC中,
,
∴△DPF≌△DQC,
∴DP=DQ,DF=DC,
∴四边形PFQC是平行四边形.
(2)如图②中,过点P作PF∥AC交BC于F,
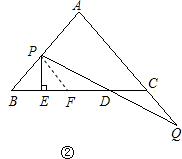
∵△PBF为等腰三角形,
∴PB=PF,
∵PE⊥BF
∴BE=EF,
由(1)可知FD=DC,
∴ED=EF+FD=
BF+
FC=
(BF+FC)=
BC=3,
∴ED为定值,

理由:∵AB=AC,
∴∠B=∠ACB,
∵PF∥AQ,
∴∠PFB=∠ACB=∠B,∠DPF=∠DQC,
∴PB=PF=CQ,
在△DPF和△DQC中,
|
∴△DPF≌△DQC,
∴DP=DQ,DF=DC,
∴四边形PFQC是平行四边形.
(2)如图②中,过点P作PF∥AC交BC于F,

∵△PBF为等腰三角形,
∴PB=PF,
∵PE⊥BF
∴BE=EF,
由(1)可知FD=DC,
∴ED=EF+FD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ED为定值,
看了 如图,在△ABC中,AB=A...的网友还看了以下:
等腰直角三角形,C为直角,AC=BC,D为BC的中点,连接AD,过C作AD的垂线,交AB于E,求证 2020-04-25 …
如图,在平行四边形ABCD中,下列结论中错误的是()A.∠1=∠2B.∠BAD=∠BCDC.AB= 2020-05-13 …
如图:在三角形ABC中,AD垂直于BC,BE垂直于AC,BC=12,AC=8,AD=6,求BE的长 2020-05-17 …
BE是圆O的直径,AC.BC相交于点C,AC,BC与圆O分别相切于点D,B,AC,BC交圆O于点D 2020-06-03 …
在Rt△ABC中,∠B=90°,∠A=α,BD是斜边AC上的高,那么()A.AC=BC•sinαB 2020-06-13 …
对任意实数a、b、c,在下列命题中,真命题是()A.“ac>bc”是“a>b”的必要条件B.“ac 2020-07-15 …
已知:如图,AB=AC,AB为圆O的直径,AC,BC分别交圆O于点E,D,连结ED,BE.求证DE 2020-07-21 …
三角形说理题.1题角ACB是直角,AC=BC,BE垂直CE,AD垂直CE于D,AD=2.5cm,D 2020-07-23 …
如果a=b,那么下列结论一定正确的是()A.a+c=b-cB.ac=bC.a-c=b-cD.ac=b 2020-12-23 …
如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是() 2021-01-22 …