早教吧作业答案频道 -->数学-->
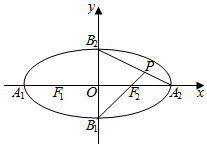
如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为.
题目详情
如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为___.

▼优质解答
答案和解析
∠B1PA2是向量
与
的夹角,
设椭圆的长半轴、短半轴、半焦距分别为a,b,c,
则向量
=(a,-b),
=(-c,-b),
∵∠B1PA2为钝角,∴-ac+b2<0,
把b2=a2-c2代入不等式得:
a2-ac-c2<0,∴1-e-e2<0,
即e2+e-1>0,
解得e<
或e>
,
又0<e<,∴
<e<1,
∴椭圆离心率的取值范围为(
,1).
故答案为:(
,1).
| B2A2 |
| F2B1 |
设椭圆的长半轴、短半轴、半焦距分别为a,b,c,
则向量
| B2A2 |
| F2B1 |
∵∠B1PA2为钝角,∴-ac+b2<0,
把b2=a2-c2代入不等式得:
a2-ac-c2<0,∴1-e-e2<0,
即e2+e-1>0,
解得e<
-1-
| ||
| 2 |
| ||
| 2 |
又0<e<,∴
| ||
| 2 |
∴椭圆离心率的取值范围为(
| ||
| 2 |
故答案为:(
| ||
| 2 |
看了 如图,椭圆的中心在原点,顶点...的网友还看了以下:
三角形ABC中,三边分别为abc,有a2=b2+c2-2bccosA,b2=a2+c2-2acco 2020-04-11 …
a,b为正数,a≠b,x,y∈(0,+∞),求证a2/x+b2/y>=(a+b)2/x+y1.求证 2020-06-12 …
设f(t)是[-k,k]上的连续函数,试证:∭x2+y2+z2≤1f(ax+by+cz)dxdyd 2020-06-22 …
在三角形ABC中,有(a2-b2)SinC/c2Sin(A-B)= 2020-07-09 …
在△ABC中,a2+b2-mc2=0(m为常数),且cosAsinA+cosBsinB=cosCs 2020-07-27 …
有下面的判断:①△ABC中,a2+b2≠c2,则△ABC不是直角三角形.②△ABC是直角三角形,∠ 2020-07-29 …
等差数列{an}中,公差不等于0,等比数列{bn}中,b1=a2,b2=a3,b3=a6求:(1) 2020-07-29 …
已知圆内接四边形ABCD的边长分别为AB=2.BC=6,CD=DA=4,求四边形ABCD的面积在三 2020-08-03 …
在△ABC中,a2=b2+c2+bc,2b=3c,a=319,则△ABC的面积为. 2020-10-31 …
在△ABC中,a2+b2=dc2,且1tanC=1005(1tanA+1tanB),则常数d的值等于 2021-01-23 …