早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点O为坐标原点,点B在x轴正半轴上,且OB=2.(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标.(2)已知,点M(m,0)、N(0
题目详情
在平面直角坐标系中,点O为坐标原点,点B在x轴正半轴上,且OB=2.
(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标.
(2)已知,点M(m,0)、N(0,n)(2<n<4),将点B向上平移2个单位长度后得到点B′,若∠MB′N=90°,且mn=
,求m2+n2的值.
(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标.
(2)已知,点M(m,0)、N(0,n)(2<n<4),将点B向上平移2个单位长度后得到点B′,若∠MB′N=90°,且mn=
| 15 |
| 7 |
▼优质解答
答案和解析
(1)如图1:
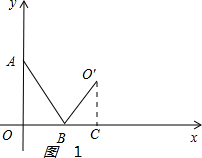
过点O′作O′C⊥x轴,垂足为点C,
∵△ABO和△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠ABO=∠ABO′,OB=O′B=2,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=∠ABO′=60°,
∵∠OBO′+∠O′BC=180°,
∴∠O′BC=60°,
∵O′C⊥x轴,
∴∠O′CB=90°,
∴∠BO′C=30°,
∴BC=
O′B=1,
∴OC=OB+BC=3,
即点O′的横坐标为:3;
2)如图2:
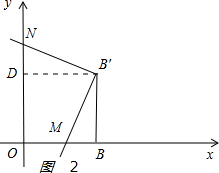
过点B′作B′D⊥y轴,垂足为点D,
∵点B在x轴正半轴上,且OB=2,
∴B(2,0),
∵点B向上平移2个单位长度后得到点B′,
∴B′(2,2),
∴BB′=B′D=2,
∵∠B′BM=90°,∠DOB=90°,∠B′DO=90°,
∴∠DB′B=90°,
∴∠DB′M+∠BB′M=90°,
∵∠MB′N=90°,
∴∠DB′M+∠DB′N=90°,
∴∠DB′N=∠BB′M,
在△DB′N和△BB′M中,
,
∴△DB′N≌△BB′M(ASA),
∴DN=BM,
∵点M(m,0),N(0,n),
∴BM=2-m,DN=n-2,
∴2-m=n-2,
即m+n=4,
∵mn=
,
∴m2+n2
=(m+n)2-2mn
=42-2×
=16-
=
.

过点O′作O′C⊥x轴,垂足为点C,
∵△ABO和△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠ABO=∠ABO′,OB=O′B=2,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=∠ABO′=60°,
∵∠OBO′+∠O′BC=180°,
∴∠O′BC=60°,
∵O′C⊥x轴,
∴∠O′CB=90°,
∴∠BO′C=30°,
∴BC=
| 1 |
| 2 |
∴OC=OB+BC=3,
即点O′的横坐标为:3;
2)如图2:

过点B′作B′D⊥y轴,垂足为点D,
∵点B在x轴正半轴上,且OB=2,
∴B(2,0),
∵点B向上平移2个单位长度后得到点B′,
∴B′(2,2),
∴BB′=B′D=2,
∵∠B′BM=90°,∠DOB=90°,∠B′DO=90°,
∴∠DB′B=90°,
∴∠DB′M+∠BB′M=90°,
∵∠MB′N=90°,
∴∠DB′M+∠DB′N=90°,
∴∠DB′N=∠BB′M,
在△DB′N和△BB′M中,
|
∴△DB′N≌△BB′M(ASA),
∴DN=BM,
∵点M(m,0),N(0,n),
∴BM=2-m,DN=n-2,
∴2-m=n-2,
即m+n=4,
∵mn=
| 15 |
| 7 |
∴m2+n2
=(m+n)2-2mn
=42-2×
| 15 |
| 7 |
=16-
| 30 |
| 7 |
=
| 82 |
| 7 |
看了 在平面直角坐标系中,点O为坐...的网友还看了以下:
阅读下面丰子恺的漫画《跌一跤,且坐坐》,请说说其中的含义。 2020-06-26 …
欣赏丰子恺漫画《跌一交,且坐坐》,回答问题。(4分)⑴写一小段话,向没看过这幅漫画的人简要介绍漫画 2020-06-26 …
在平面直角坐标系xOy中,曲线C1的参数方程为x=1+cosαy=1+sinα(其中α为参数).在 2020-07-09 …
怎样把直角坐标系的方程转化成极坐标方程?最近很纳闷!在做二次曲线积分是遇到一个难题:怎么把一般的直 2020-07-20 …
关于人体衰老细胞和癌细胞的叙述,正确的是()A.癌细胞与衰老细胞都有基因表达B.癌变和衰老都是细胞 2020-07-25 …
设直线l1:y=2x与直线l2:x+y=3交于P点.(1)当直线m过P点,且与直线l0:x-2y= 2020-07-30 …
在直角坐标系xOy中,曲线c1的参数方程为:(θ为参数),把曲线c1上所有点的纵坐标压缩为原来的一 2020-07-31 …
(选修4--4:坐标系与参数方程)在直角坐标系xoy中,曲线M的参数方程为x=sinθ+cosθy 2020-07-31 …
如图所示在平面直角坐标系xoy中,第I象限存在沿y轴负方向的匀强电场,第IV象限存在垂直于坐标平面 2020-07-31 …
阅读丰子恺漫画《跌一跤,且坐坐》,回答问题。(4分)(1)简要说明漫画的主要内容。(2分)答: 2020-12-09 …