早教吧作业答案频道 -->数学-->
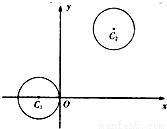
如图,在平面直角坐标系xOy中,已知圆,圆.(1)若过点C1(-1,0)的直线l被圆C2截得的弦长为,求直线l的方程;(2)设动圆C同时平分圆C1的周长、圆C2的周长.①证明:动
题目详情
如图,在平面直角坐标系xOy中,已知圆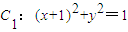 ,圆
,圆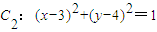 .
.
(1)若过点C 1 (-1,0)的直线l被圆C 2 截得的弦长为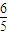 ,求直线l的方程;
,求直线l的方程;
(2)设动圆C同时平分圆C 1 的周长、圆C 2 的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
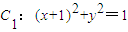 ,圆
,圆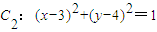 .
.(1)若过点C 1 (-1,0)的直线l被圆C 2 截得的弦长为
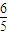 ,求直线l的方程;
,求直线l的方程;(2)设动圆C同时平分圆C 1 的周长、圆C 2 的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.

▼优质解答
答案和解析
分析:
(1)设过直线l方程:y=k(x+1),根据垂直于弦的直径的性质,结合点到直线的距离公式列式,可解出k的值,从而得到直线l的方程;(2)①由题意,圆心C到C1、C2两点的距离相等,由此结合两点间的距离公式建立关系式,化简整理得x+y-3=0,即为所求定直线方程;②根据题意设C(m,3-m),得到圆C方程关于参数m的一般方程形式,由此可得动圆C经过圆x2+y2-6y-2=0与直线x-y+1=0的交点,最后联解方程组,即可得到动圆C经过的定点坐标.
(1)设过点C1(-1,0)的直线l方程:y=k(x+1),化成一般式kx-y+k=0∵直线l被圆C2截得的弦长为,∴点C2(3,4)到直线l的距离为d==,解之得k=或由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.(2)①设圆心C(x,y),由题意,得CC1=CC2,即=,化简整理,得x+y-3=0,即动圆圆心C在定直线x+y-3=0上运动.②设圆C过定点,设C(m,3-m),则动圆C的半径为=,于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,整理,得x2+y2-6y-2-2m(x-y+1)=0,由得或所以动圆C经过定点,其坐标为,.
点评:
本题求被定圆截得定长的弦所在直线方程,并探索动圆圆心在定直线上的问题.考查了直线与圆的方程、直线与圆和圆与圆的位置关系,考查学生运算能力.
分析:
(1)设过直线l方程:y=k(x+1),根据垂直于弦的直径的性质,结合点到直线的距离公式列式,可解出k的值,从而得到直线l的方程;(2)①由题意,圆心C到C1、C2两点的距离相等,由此结合两点间的距离公式建立关系式,化简整理得x+y-3=0,即为所求定直线方程;②根据题意设C(m,3-m),得到圆C方程关于参数m的一般方程形式,由此可得动圆C经过圆x2+y2-6y-2=0与直线x-y+1=0的交点,最后联解方程组,即可得到动圆C经过的定点坐标.
(1)设过点C1(-1,0)的直线l方程:y=k(x+1),化成一般式kx-y+k=0∵直线l被圆C2截得的弦长为,∴点C2(3,4)到直线l的距离为d==,解之得k=或由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.(2)①设圆心C(x,y),由题意,得CC1=CC2,即=,化简整理,得x+y-3=0,即动圆圆心C在定直线x+y-3=0上运动.②设圆C过定点,设C(m,3-m),则动圆C的半径为=,于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,整理,得x2+y2-6y-2-2m(x-y+1)=0,由得或所以动圆C经过定点,其坐标为,.
点评:
本题求被定圆截得定长的弦所在直线方程,并探索动圆圆心在定直线上的问题.考查了直线与圆的方程、直线与圆和圆与圆的位置关系,考查学生运算能力.
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
小方骑自行车,每时行xKm,小园骑自行车的速度是小方的1.5倍.1.5x表示什么?3x又表示什么? 2020-03-31 …
已知直线L:y=-1/2x+m与曲线c:y=1+(1/2)*(√|4-x²|)仅有三个交点,则实数 2020-05-15 …
(1+x乘e的x次方)的1/x次方 的极限(x趋近于0) 2020-05-16 …
把54本书分给三个组,A组的1/2和B组的1/3和C组的1/4相等,ABC个分多少书? 2020-06-14 …
我算了算,泛音列的顺序和分音列分段振动数不是一致的啊比如有一根弦.空弦是c弦的1/2是高音c1/3 2020-06-26 …
求这些古诗都是什么地方的1、水光潋滟晴方好,山色空蒙雨亦奇.2、举头红日近,俯首白云低.3、先天下 2020-06-26 …
半坡遗址是那个地方的1长江2黄河3珠江4松花江4选1 2020-06-26 …
应用:现有A、B、C三桶油,先把A桶的1/3倒入B桶,再把B桶的1/4倒入C桶,最后把C桶的1/1 2020-06-27 …
公路全长360米,甲方和乙方同时修路,甲方修路的速度是乙方的1.25倍,4天后路请问甲乙双方平均每 2020-06-27 …
甲、乙两个乒乓球队进行一次乒乓球擂台赛,双方各派出水平相当的3名选手按事先排好的顺序出场比赛,先有 2020-07-02 …