早教吧作业答案频道 -->数学-->
如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(
题目详情
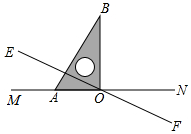
如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,EF平分∠AOB?
②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,EF平分∠AOB?
②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.
▼优质解答
答案和解析
(1)∵当直角边OB恰好平分∠NOE时,∠NOB=
∠NOE=
(180°-30°)=75°,
∴90°-3t°=75°,
解得:t=5.
此时∠MOA=3°×5=15°=
∠MOE,
∴此时OA平分∠MOE.
(2)①OE平分∠AOB,
依题意有30°+9t-3t=90°÷2,
解得t=2.5;
OF平分∠AOB,
依题意有30°+9t-3t=180°+90°÷2,
解得t=32.5.
故当t为2.5s或32.5s时,EF平分∠AOB
②OB在MN上面,
依题意有180°-30°-9t=(90°-3t)÷2,
解得t=14;
OB在MN下面,
依题意有9t-(360°-30°)=(3t-90°)÷2,
解得t=38.
故EF能平分∠NOB,t的值为14s或38s.
| 1 |
| 2 |
| 1 |
| 2 |
∴90°-3t°=75°,
解得:t=5.
此时∠MOA=3°×5=15°=
| 1 |
| 2 |
∴此时OA平分∠MOE.
(2)①OE平分∠AOB,
依题意有30°+9t-3t=90°÷2,
解得t=2.5;
OF平分∠AOB,
依题意有30°+9t-3t=180°+90°÷2,
解得t=32.5.
故当t为2.5s或32.5s时,EF平分∠AOB
②OB在MN上面,
依题意有180°-30°-9t=(90°-3t)÷2,
解得t=14;
OB在MN下面,
依题意有9t-(360°-30°)=(3t-90°)÷2,
解得t=38.
故EF能平分∠NOB,t的值为14s或38s.
看了 如图,直线EF与MN相交于点...的网友还看了以下:
初中数学竞赛几何证明题已知点o为等边三角形ABC的内心,直线m过点o,过A、B、C三点分别作直线m 2020-05-16 …
1.已知直线y=(m-2)x-3与直线y=((5-m)/2)*x+m平行,求m的值.此时这两条直线 2020-06-02 …
直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点 2020-07-30 …
设直线l1:y=2x与直线l2:x+y=3交于P点.(1)当直线m过P点,且与直线l0:x-2y= 2020-07-30 …
已知一次函数y=3+m(O<m≤1)的图象为直线l,直线l绕原点O旋转180°后得直线l',△ABC 2020-11-10 …
(2006•淮安)已知一次函数y=3+m(O<m≤1)的图象为直线l,直线l绕原点O旋转180°后得 2020-11-12 …
1.求面积为m(m>o)的正三角形的周长2.求三个数a,b,c中的最大数3.判断直线Ax+By+C= 2020-11-20 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …
如图,已知在平面直角坐标系内直线y=-3/4x+3分别与x轴、y轴相交于点A和点B,直线m为过点O的 2020-12-25 …