如图，在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An=1（n为正整数），过点A1，A2，A3，…，An分别作y轴的垂线，与反比例函数y=2x（x>0）交于P1，P2，P3，…，Pn，连接P1P2，P2P

Question

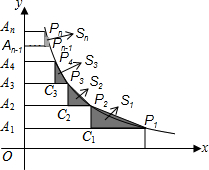
如图，在y轴正半轴上依次截取OA₁=A₁A₂=A₂A₃=…=A_n-1A_n=1（n为正整数），过点A₁，A₂，A₃，…，A_n分别作y轴的垂线，与反比例函数y= (2)/(x)（x>0）交于P₁，P₂，P₃，…，P_n，连接P₁P₂，P₂P₃，P₃P₄，…，P_n-1P_n，过点P₂、P₃、…、P_n分别向P₁A₁、P₂A₂、…、P_n-1A_n-1作垂线段，构成一列三角形（见图中阴影部分），记这一系列三角形的面积分别为S₁，S₂，S₃，…，S_n，则S₁+S₂+S₃+…+S_n-1=___．

Answer 1

∵OA₁=A₁A₂=A₂A₃=…=A_n-1A_n=1，
∴设P₁（x₁，1），P₂（x₂，2），P₃（x₃，3），…P_n（x_n，n），
∵P₁，P₂，P₃…Pn在反比例函数y=(2)/(x)（x>0）的图象上，
∴x₁=2，x₂=1，x₃=(2)/(3)…x_n=(2)/(n)，
∴S₁=(1)/(2)×（x₁-x₂）×1=(1)/(2)×1×（2-1）=1-(1)/(2)；
S₂=(1)/(2)×1×（x₂-x₃）=(1)/(2)×1×（1-(2)/(3)）=(1)/(2)-(1)/(3)；
S₃=(1)/(2)×1×（x₃-x₄）=(1)/(2)×1×（(2)/(3)-(1)/(2)）=(1)/(3)-(1)/(4)；
…
S_n-1=(1)/(2)（(2)/(n-1)-(2)/(n)），
∴S₁+S₂+S₃+…+S_n-1=1-(1)/(2)+(1)/(2)-(1)/(3)+(1)/(3)-(1)/(4)+…+(1)/(n-1)-(1)/(n)=1-(1)/(n)．
故答案为：1-(1)/(n)．