(本小题满分14分)已知椭圆的中心在坐标原点,两个焦点分别为,,点在椭圆上,过点的直线与抛物线交于两点,抛物线在点处的切线分别为,且与交于点.(1)求椭圆的方程;(2)
(本小题满分14分)
已知椭圆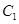 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为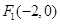 ,
,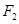
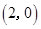 ,点
,点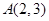 在椭圆
在椭圆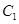 上,过点
上,过点 的直线
的直线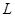 与抛物线
与抛物线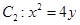 交于
交于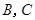 两点,抛物线
两点,抛物线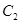 在点
在点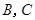 处的切线分别为
处的切线分别为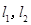 ,且
,且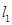 与
与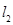 交于点
交于点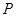 .
.
(1) 求椭圆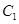 的方程;
的方程;
(2) 是否存在满足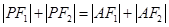 的点
的点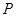 ? 若存在,指出这样的点
? 若存在,指出这样的点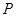 有几个(不必求出点
有几个(不必求出点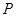 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
一道常微分方程我用全微分法中的两种方法算出来不一样这个方程是恰当方程,然后我用书上给的这两个公式算 2020-04-25 …
急用:图像处理中英文文献有变分矩阵,分为水平和垂直方向的一阶微分,具体是什么样的主要想问下图像在i 2020-05-13 …
1.时分,两组同学到村外平坦的田野中采集植物标本,分手后,他们向不同的两个方向前进,第一组的速度是 2020-05-15 …
概率论中二维随机变量求边缘密度的两种方法的问题……看这个题目:二维随机变量的联合分布函数满足:F( 2020-05-17 …
急.这种“2阶”的微分方程怎么积啊?d2y---=ydx2大概说下积分的方法就可以了普通一阶的微分 2020-06-18 …
某医院对治疗支气管肺炎的两种方案A,B进行比较研究,将志愿者分为两组,分别采用方案A和方案B进行治 2020-06-22 …
探究压力的作用效果与受力面积的关系时,分别采用如图甲、乙所示的两种方法.用两只手的食指分别压在铅笔 2020-07-21 …
求解可分离变量的微分方程的方法为:(1)将方程分离变量得到:dyg(y)=f(x)dx;(2)等式 2020-08-02 …
英语翻译网球比赛的计分方式与其他比赛的计分方式与众不同.其他比赛都是以1分来计分的.而网球是胜1分叫 2020-10-30 …
Draw2D和JGraph是什么关系啊,两个分别属于什么范畴?是图形处理的两种方式吗?谢谢!Draw 2020-11-07 …