早教吧作业答案频道 -->数学-->
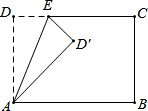
如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为.
题目详情
如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为___.

▼优质解答
答案和解析
如图1,
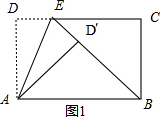
∵折叠,
∴△AD′E≌△ADE,
∴∠AD′E=∠D=90°,
∵∠AD′B=90°,
∴B、D′、E三点共线,
又∵ABD′∽△BEC,AD′=BC,
∴ABD′≌△BEC,
∴BE=AB=17,
∵BD′=
=
=15,
∴DE=D′E=17-15=2;
如图2,
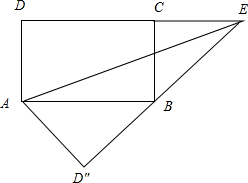
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
,
∴△ABD″≌△BEC,
∴BE=AB=17,
∴DE=D″E=17+15=32.
综上所知,DE=2或32.
故答案为:2或32.

∵折叠,
∴△AD′E≌△ADE,
∴∠AD′E=∠D=90°,
∵∠AD′B=90°,
∴B、D′、E三点共线,
又∵ABD′∽△BEC,AD′=BC,
∴ABD′≌△BEC,
∴BE=AB=17,
∵BD′=
| AB2-AD′2 |
| 172-82 |
∴DE=D′E=17-15=2;
如图2,

∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
|
∴△ABD″≌△BEC,
∴BE=AB=17,
∴DE=D″E=17+15=32.
综上所知,DE=2或32.
故答案为:2或32.
看了 如图,长方形ABCD中,∠D...的网友还看了以下:
平面直角坐标系内的点P(x,y)关于下列点或直线对称的点坐标对称中心对称点的坐标(0,0)———— 2020-05-02 …
用托盘天平称量易潮解的药品时,正确的方法是将易潮解的药品()A.直接放在干燥的小烧杯里称量B.直接 2020-05-17 …
函数f(x)=a^|x-b|(a>0,且a≠1)的图像关于直线X=b对称函数f(x)=a|x-b| 2020-05-22 …
求证:1,若函数y=f(x)(x∈R)的图像关于(a,0)与直线x=b(b>a)对称,则T=4|b 2020-06-05 …
在极坐标系中,曲线p=4sin(θ-π/3)关于A.直线θ=派/3对称B.直线θ=5/6派对称C. 2020-06-27 …
一次函数y=kx+b(k≠0)中k、b的意义:k(称为斜率)表示直线y=kx+b(k≠0)的倾斜程 2020-06-30 …
1.f(x)与f(2a-x)关于直线x=a对称能得出f(x)与f(2a-x)关于直线x=a上任意一 2020-08-01 …
两个图形关于某直线对称,对称点一定在()A.直线的两旁B.直线的同旁C.直线上D.直线两旁或直线上 2020-08-01 …
关于点与直线设点P(Xo,Yo)是直角坐标系内任意一点,则点P(1)关于直线X=a的对称点为(,) 2020-08-01 …
等腰三角形有一条对称轴这句话对不对本题原样:以下语句哪个是错的?A,等腰三角形有一条对称轴B,直线是 2021-02-02 …