早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.(1)求∠DAE的度数;(2)若正方形ABCD的边长为1,求等边三角形AEF的面积;(3)将△AEF绕着点E逆时针旋转m
题目详情
如图,已知四边形ABCD是正方形,△AEF是等边三角形,E、F分别位于DC边和BC边上.
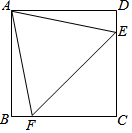
(1)求∠DAE的度数;
(2)若正方形ABCD的边长为1,求等边三角形AEF的面积;
(3)将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.

(1)求∠DAE的度数;
(2)若正方形ABCD的边长为1,求等边三角形AEF的面积;
(3)将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.
▼优质解答
答案和解析
(1)∵四边形ABCD是正方形,
∴AB=AD,AF=AE,∠B=∠D=90°,
在Rt△ABF与Rt△ADE,
,
∴Rt△ABF≌Rt△ADE,
∴∠DAE=∠BAF
又∠DAE+∠BAF=∠BAD-∠EAF=90°-60°=30°
∴∠DAE=15°;
(2)设BF=x,由(1)可知DE=BF=x,则,CF=CE=1-x
AB2+BF2=AF2,CF2+CE2=EF2,AF=EF,得:12+x2=2(1-x)2
x1=2+
,x2=2-
,
∵0<x<1,
∴x1=2+
(舍去),x=2-
,
∴S△AEF=S四边形ABCD-2S△ABF-S△EFC=12-2×
×1×(2-
)-
×(
-1)2=2
-3;
(3)依题意,点A可落在AB边上或BC边上.
当点A落在AB边上时,设此时点A的对应点为M,则EA=EM,
∵∠EAB=75°,
∴∠EMB=75°,
∴m=∠AEM=180°-75°-75°=30°,
当点A落在边BC上时,
∵EA=EF,点A旋转后与点F重合,
∴m=∠AEF=60°,
综上,m=30°或m=60°.
∴AB=AD,AF=AE,∠B=∠D=90°,
在Rt△ABF与Rt△ADE,
|
∴Rt△ABF≌Rt△ADE,
∴∠DAE=∠BAF
又∠DAE+∠BAF=∠BAD-∠EAF=90°-60°=30°
∴∠DAE=15°;
(2)设BF=x,由(1)可知DE=BF=x,则,CF=CE=1-x
AB2+BF2=AF2,CF2+CE2=EF2,AF=EF,得:12+x2=2(1-x)2
x1=2+
| 3 |
| 3 |
∵0<x<1,
∴x1=2+
| 3 |
| 3 |
∴S△AEF=S四边形ABCD-2S△ABF-S△EFC=12-2×
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
(3)依题意,点A可落在AB边上或BC边上.
当点A落在AB边上时,设此时点A的对应点为M,则EA=EM,
∵∠EAB=75°,
∴∠EMB=75°,
∴m=∠AEM=180°-75°-75°=30°,
当点A落在边BC上时,
∵EA=EF,点A旋转后与点F重合,
∴m=∠AEF=60°,
综上,m=30°或m=60°.
看了 如图,已知四边形ABCD是正...的网友还看了以下:
如图,M是四边形ABCD的对角线AC上的点,ME∥CD,MF∥BC,MCMA=13.(1)求证:四 2020-05-13 …
如图,M是四边形ABCD的对角线AC上的点,ME∥CD,MF∥BC,MCMA=13.(1)求证:四 2020-05-13 …
如图,M是四边形ABCD的对角线AC上的点,ME∥CD,MF∥BC,MCMA=13.(1)求证:四 2020-06-13 …
已知:一次函数y=3/2x+m 如果它的图像经过第一三四象限,且与坐标轴围成的三角形面积为27,求 2020-06-27 …
如图,已知▱ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作▱ABC 2020-07-09 …
如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D( 2020-07-22 …
如图,已知圆O的圆心为O,半径为3,点M为圆O内的一个定点,OM=5,AB、CD是圆O的两条相互垂 2020-07-24 …
一元二次方程高手进㎡-5丨m丨+k=0如果方程有四个实数根求k和m如果只有三个实数根求k和m 2020-08-02 …
如图1已知抛物线y=x2-ax+b与x轴交于A、B两点,与y轴交于点C,顶点D的坐标为(1,-4)( 2020-11-27 …
excel的高手进来求救!E(四月应付)F(四月实付)G(四月应付未付)H(四月余额)K(五月应付) 2020-12-14 …