早教吧作业答案频道 -->数学-->
如图,长方形ABCD的面积为120平方厘米,BE=3AE,BF=2FC,则S△AEG=.
题目详情
如图,长方形ABCD的面积为120平方厘米,BE=3AE,BF=2FC,则S△AEG=___.
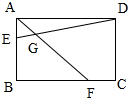

▼优质解答
答案和解析
如图,延长DC、AF相交于点H,
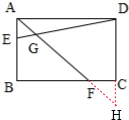
因为ABCD是长方形,
所以AB∥DH,
所以△HCF∽△ABF,△AEG∽HDG,
所以
=
,
=
因为BE=3AE,BF=2FC,
所以AE=
AB,CH=
AB,
所以AE:DH=1:6,
(AE占1份,EB占4份,AB=CD,占5份,DH占6份)
所以EG:GD=1:6,
因为△AED的面积=
AB×AD÷2,长方形ABCD的面积是120平方厘米,
所以△AED的面积=
×120÷2
=15(平方厘米),
(
×AB×AD÷2,AB×AD=长方形ABCD的面积=120平方厘米)
又因为△AEG与△AGD的面积比是1:6,
所以△AEG的面积=15÷(6+1)
=
(平方厘米).
故答案为:
平方厘米.

因为ABCD是长方形,
所以AB∥DH,
所以△HCF∽△ABF,△AEG∽HDG,
所以
| HC |
| AB |
| CF |
| BF |
| AE |
| DH |
| EG |
| GD |
因为BE=3AE,BF=2FC,
所以AE=
| 1 |
| 4 |
| 1 |
| 2 |
所以AE:DH=1:6,
(AE占1份,EB占4份,AB=CD,占5份,DH占6份)
所以EG:GD=1:6,
因为△AED的面积=
| 1 |
| 4 |
所以△AED的面积=
| 1 |
| 4 |
=15(平方厘米),
(
| 1 |
| 4 |
又因为△AEG与△AGD的面积比是1:6,
所以△AEG的面积=15÷(6+1)
=
| 15 |
| 7 |
故答案为:
| 15 |
| 7 |
看了 如图,长方形ABCD的面积为...的网友还看了以下:
1.若a>0,b>0,则|ab|=();若a>0,b<0,则|ab|=();若a<0,b>0,则| 2020-04-06 …
设A,B为n阶方阵,且满足等式AB=0,则必有(A)A=0或B=0(B)A+B=0(C)|A|=0 2020-06-18 …
若a大于b大于c,且a+c+b=0,则下列不等式中正确的是A,ab大于acB,a若a大于b大于c, 2020-08-03 …
求个公式,知道的告诉下,如果A>0,则Z等于A*0.45如果B>0,则Z等于B*0.15如果C>0, 2020-11-01 …
设A,B为n阶矩阵,则下列结论中正确的是A:若AB=0,则BA=0B:若AB=0,且B≠0,则IAI 2020-11-02 …
定义运算a*b=a(1-b),下面给出了几个结论:1.a*b=b*a2.若a+b=0,则(a*a)+ 2020-11-08 …
(1)若导线头E接在d点时,电压表示数为4.5V,而接在c点时,电压表示数为0,则d、c之间的电压是 2020-11-17 …
1.阅读下面的文字,5的相反数是-5,则5+(-5)=0;1/3的相反数是-1/3,则1/3+(-1 2020-11-20 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …
1.下列命题中正确的是().A.若向量a*向量b=0,则向量a=0或向量b=0.B.若向量a*向量b 2020-12-18 …