早教吧作业答案频道 -->数学-->
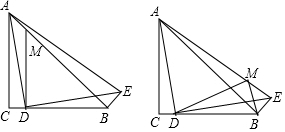
若D为等腰直角三角形ABC的BC边上任一点,且DE⊥AD,BE⊥AB.(1)求证:△ADE是等腰直角三角形;(2)如图,当D在CB上任意运动时,若BC=a,过B作BM⊥BC交AE于M,现给二个结论:①∠BMD的度数不
题目详情
若D为等腰直角三角形ABC的BC边上任一点,且DE⊥AD,BE⊥AB.
(1)求证:△ADE是等腰直角三角形;
(2)如图,当D在CB上任意运动时,若BC=a,过B作BM⊥BC交AE于M,现给二个结论:①∠BMD的度数不变:②BD+BM+DM值不变,其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论,并求其值.
(1)求证:△ADE是等腰直角三角形;
(2)如图,当D在CB上任意运动时,若BC=a,过B作BM⊥BC交AE于M,现给二个结论:①∠BMD的度数不变:②BD+BM+DM值不变,其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论,并求其值.

▼优质解答
答案和解析
(1)证明:如图1中,在线段CA取一点F,使得CF=CD.
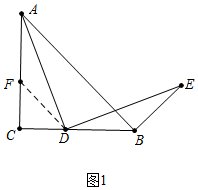
∵∠C=90°,CF=CD,AC=CB,
∴AF=DB,∠CFD=∠CDF=45°,
∴∠AFD=135°,
∵BE⊥AB,∠ABC=45°,
∴∠ABE=90°,
∴∠DBE=135°,
∴∠AFD=∠DBE,
∵AD⊥DE,
∴∠ADE=90°,
∵∠FAD+∠ADC=90°,∠ADC+∠BDE=90°,
∴∠FAD=∠BDE,
在△ADF和△DEB中,
,
∴△ADF≌△DEB.
∴AD=DE,
∵∠ADE=90°,
∴△ADE是等腰直角三角形.
(2) ②正确.
理由:如图2中,作AG⊥BM交BM的延长线于G,在BG 的延长线上截取GH=CD.
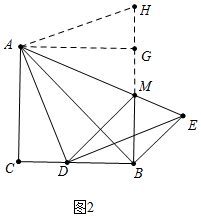
∵∠C=∠CBG=∠AGB=90°,
∴四边形ACBG是矩形,
∵AC=CB,
∴四边形ACBG是正方形,
∴AC=AG,∠ACD=∠AGH=90°,
∴△ACD≌△AGH,
∴AD=AH,∠GAH=∠CAD,
∵∠DAE=45°,
∴∠MAH=∠MAG+∠GAH=∠MAG+∠CAD=45°,
∴∠MAD=∠MAH,∵MA=MA,
∴△MAH≌△MAD,
∴DM=KM,
∵HM=GM+HG=GM+CD,
∴DM=CD+GM.
∴BD+BM+DM=BD+BM+CD+MG=BC+BG=2BC=2a.
∴BD+BM+DM的值是定值.

∵∠C=90°,CF=CD,AC=CB,
∴AF=DB,∠CFD=∠CDF=45°,
∴∠AFD=135°,
∵BE⊥AB,∠ABC=45°,
∴∠ABE=90°,
∴∠DBE=135°,
∴∠AFD=∠DBE,
∵AD⊥DE,
∴∠ADE=90°,
∵∠FAD+∠ADC=90°,∠ADC+∠BDE=90°,
∴∠FAD=∠BDE,
在△ADF和△DEB中,
|
∴△ADF≌△DEB.
∴AD=DE,
∵∠ADE=90°,
∴△ADE是等腰直角三角形.
(2) ②正确.
理由:如图2中,作AG⊥BM交BM的延长线于G,在BG 的延长线上截取GH=CD.

∵∠C=∠CBG=∠AGB=90°,
∴四边形ACBG是矩形,
∵AC=CB,
∴四边形ACBG是正方形,
∴AC=AG,∠ACD=∠AGH=90°,
∴△ACD≌△AGH,
∴AD=AH,∠GAH=∠CAD,
∵∠DAE=45°,
∴∠MAH=∠MAG+∠GAH=∠MAG+∠CAD=45°,
∴∠MAD=∠MAH,∵MA=MA,
∴△MAH≌△MAD,
∴DM=KM,
∵HM=GM+HG=GM+CD,
∴DM=CD+GM.
∴BD+BM+DM=BD+BM+CD+MG=BC+BG=2BC=2a.
∴BD+BM+DM的值是定值.
看了 若D为等腰直角三角形ABC的...的网友还看了以下:
已知角A=125°-a,角B=a-35°,则角A与角B的关系是什么A、互补B、互余C、相等D、角A 2020-04-09 …
选出下列词中[]部分发音不同的单词1.A.[a]nyB.sh[a]peC.[e]lseD.[a]n 2020-05-14 …
已知如图,平行四边形ABCD中,AB大于BC,角A和角D的平分线交于点E,角B和角C的平分线交于点 2020-05-15 …
已知三角形ABC与三角形A'B'C'中,AB=A'B',BC=B'C',角BAC=角B'C'A'= 2020-05-16 …
在四边形中,已知角A=角E,角B=角D,四边形ABCD是平行四边形吗?理由角A=角C,角A不是等于 2020-06-02 …
在平行四边形ABCD中,AB大于BC,角A与角D的平分线交于点E,角B与角C的平分线交于点F.(1 2020-06-27 …
1.已知,三角形ABC全等于三角形AED,角E=角B,角c=角ADE,写出对应边和对应角,若角BA 2020-08-01 …
已知:如图,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A.∠A与∠D互为余角 2020-08-02 …
等腰梯形证明题.在等腰梯形abcd中,AD//BC,CA平分角BCD,DE//AC.,交BC的延长 2020-08-02 …
解几何题三角形ABC中,AD平分角A交BC与D,CE平分角C交AB与E,角B=60°,求AE+CD 2020-08-02 …