早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.(1)直接写出∠ABD的大小(用含α的式子表示);(2)判断DC与CE的位置关
题目详情
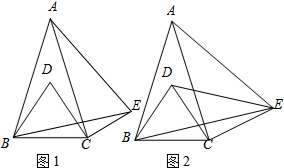
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.
(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.

▼优质解答
答案和解析
(1)∵AB=AC,∠A=∠α,
∴∠ABC=∠ACB=
(180°-∠α)
=90°-
∠α
∴∠ABD=∠ABC-∠ABE
=90°-
∠α-60°
=30°-
∠α;
(2)DC与CE垂直;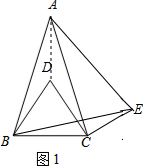
连接AD;
∵∠ABE=∠DBC=60°,
∴∠ABE-∠DBE=∠DBC-∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
,
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=
∠α,
∴∠BDA=180°-∠ABD-∠BAD=180°-(30°-
∠α )-
∠α=150°,
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直;
(3)∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=DE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°-
∠α=15°,
∴∠α=30°.
∴∠ABC=∠ACB=
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
∴∠ABD=∠ABC-∠ABE
=90°-
| 1 |
| 2 |
=30°-
| 1 |
| 2 |
(2)DC与CE垂直;

连接AD;
∵∠ABE=∠DBC=60°,
∴∠ABE-∠DBE=∠DBC-∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
|
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
|
∴△ABD≌△ACD,
∴∠BAD=∠CAD=
| 1 |
| 2 |
∴∠BDA=180°-∠ABD-∠BAD=180°-(30°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直;
(3)∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=DE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°-
| 1 |
| 2 |
∴∠α=30°.
看了 在△ABC中,AB=AC,∠...的网友还看了以下:
“无心插柳柳成荫”,“插柳”采用的方法是()A.嫁接B.分根C.扦插D.杂交 2020-05-13 …
三角形ABC的内角A,B,C所对的边分别为a,b,c,它的外接圆半径为6,三边a,b,c,角A,B 2020-05-16 …
在三角形ABC中,AC等于BC,角ACB等于90度将三角形ABC绕点C逆时针旋转a角,得到三角形A 2020-05-17 …
(1/2)已知三角形ABC的外接圆半径为R,角ABC的对边为abc.且cos2分之C=sin(A+ 2020-06-02 …
信贷档案管理应做到( )。A.分段管理、专人负责、按时交接 B.分段管理、专人负责、定点交接 2020-06-27 …
初一数学求证题如图三角形ABC中AB=ACBD=BC角1等于角2求证三角形ABD是等腰三角形不能传 2020-06-27 …
几何方面的问题三角形ABC的三个顶点都在同一圆上,根据圆周角定理得:角C是弧AB所对应的圆心角的二 2020-08-01 …
已知三角形ABC中,AB=12,AC=18,NM平行BC,BE平分角ABC,CE平分角ACB,求三角 2020-11-27 …
如图所示,已知DE平行BC,EF平行AB,那么角B与角DEF有什么关系?理由绘图:是个三角形三个顶点 2020-12-12 …
已知三角形ABC的内角A,B,C所对的边分别为a,b,c,.已知三角形ABC的内角A,B,C所对的边 2021-02-07 …